Проблема представления данных

Приближенные вычисления.

Хотя выше и отмечалось, что в компьютерной алгебре вычисления обычно производятся точно, без округления, тем не менее в ней рассматриваются и задачи, требующие приближенного решения (например, нахождение вещественных корней многочлена). В отличие от численного анализа ответ в таких задачах представляется не в виде числа, а в виде интервала на вещественной оси (области в комплексной плоскости). С такими интервалами можно производить арифметические действия, соответствующая арифметика известна под названием интервальной. Как правило, интервальная арифметика комбинируется с арифметикой многократной точности, поскольку требуемая точность обычно весьма высока.

Когда мы говорим о приближенных вычислениях, то подразумеваем, что определено понятие cходимости. Из курса математического анализа известно, что поле вещественных чисел можно определить как пополнение поля рациональных чисел по архимедовой метрике, когда расстояние между двумя рациональными числами определяется как модуль их разности. В математике, в частности, в теории чисел, рассматриваются также другие метрики поля рациональных чисел, так называемые p -адические. При пополнении поля по p -адической метрике получается поле p -адических чисел. Некоторые сведения о таких полях приведены в лекциях "Проблема представления данных" , "Наибольший общий делитель и последовательности полиномиальных остатков" .

При вычислениях с вещественными числами мы, в действительности, имеем дело обычно с их приближенными значениями, которые представляют собой десятичные (или двоичные, при использовании компьютера) дроби с фиксированным числом значащих цифр. При работе с приближенными значениями p -адических чисел получаются объекты, которые известны как коды Гензеля. Их описание можно найти в специальной литературе, например, [ 5 ] .

1.7. УПРАЖНЕНИЯ.

1. Привести пример аксиомы поля вещественных чисел, не выполняющейся при работе с числами типа float на языке Си.
2. Какие аксиомы поля вещественных чисел не выполняются при работе с числами типа float на языке Си?
3. Привести пример аксиомы поля вещественных чисел, не выполняющейся для интервальной арифметики.
4. Какие аксиомы поля вещественных чисел не выполняются для интервальной арифметики?

Алгебраические числа.

1.8. ОПРЕДЕЛЕНИЕ. Алгебраическим числом называется число , являющееся корнем многочлена от одной переменной с целыми коэффициентами. Если старший коэффициент этого многочлена равен 1, то алгебраическое число называется целым.

1.9. ПРЕДЛОЖЕНИЕ. Существуют алгебраические числа, не выражающиеся через радикалы.

Доказательство этого утверждения основано на теории Галуа и может быть найдено в учебниках по алгебре.

Таким образом, в поле алгебраических чисел можно выделить подполя алгебраических чисел, порожденных простыми радикала ми ( простые радикальные расширения ) и вложенными радикалами ( вложенные радикальные расширения ), а также соответствующие подкольца в кольце целых алгебраических чисел.

Представление алгебраических чисел представляет собой значительно более трудную задачу. Если речь идет об одном алгебраическом числе, то для его задания нужно знать минимальный многочлен, корнем которого является данное число. В большинстве алгебраических задач несущественно различие между различными корнями одного и того же неприводимого многочлена. Однако в задачах, где используются различные метрические свойства, часто приходится для задания алгебраического числа указывать не только соответствующий неприводимый многочлен, но и интервал на вещественной оси или область в комплексном пространстве, содержащую единственный корень указанного многочлена. При этом арифметические операции над алгебраическими числами оказываются очень трудоемкими. Нахождение минимального многочлена для суммы или произведения алгебраических чисел представляет собой нетривиальную задачу, методы его нахождения будут описаны ниже, при изучении базисов Гребнера.

При работе с конкретным полем алгебраических чисел используется представление чисел этого поля, связанное с фиксированием примитивного элемента и с однозначностью представления элементов этого поля через фиксированный примитивный элемент. Упомянутые выше сложности возникают при необходимости производить операции над элементами из различных конечных расширений поля рациональных чисел. Эти сложности настолько значительны, что часто приходится отказываться от выбора примитивного элемента и рассматривать поля алгебраических чисел как расширения поля рациональных чисел с многими образующими. В частности, такое представление обычно используется при работе с радикальными расширениями, т. е. с расширениями поля рациональных чисел, получаемыми последовательным присоединением радикалов некоторых элементов (возможно, с вложениями).

1.10. УПРАЖНЕНИЯ.

1. Показать, что 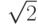, , 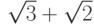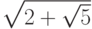— целые алгебраические числа.
2. Показать, что целые алгебраические числа образуют кольцо.
3. Показать, что алгебраические числа образуют поле.
4. Найти минимальный многочлен над для .
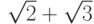5. Построить каноническое представление для элементов поля .
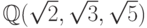6. Построить алгоритм получения канонического представления для простых радикальных расширений (полей алгебраических чисел, порожденных несколькими радикалами без вложений).
7. Построить алгоритм получения канонического представления для вложенных радикальных расширений.

Трансцендентные числа.

Большинство систем компьютерной алгебры допускает работу с трансцендентными числами e и 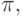для которых фиксированы соответствующие свойства тригонометрических, логарифмических и показательных функций. Вычисления в трансцендентных расширениях производятся так же, как в полях рациональных функций. Задание конкретного трансцендентного числа какими-либо метрическими или функциональными свойствами и проверка его алгебраической независимости с уже имеющимися величинами представляет собой алгоритмически неразрешимую задачу.