|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Паросочетания
Метод увеличивающих путей
Пусть  - граф,
- граф,  - некоторое
паросочетание в нем. Ребра
паросочетания будем называть сильными, остальные ребра графа - слабыми. Вершину назовем свободной, если она не принадлежит ребру
паросочетания. На рис. 12.1 слева
показан граф
и в нем выделены ребра паросочетания
- некоторое
паросочетание в нем. Ребра
паросочетания будем называть сильными, остальные ребра графа - слабыми. Вершину назовем свободной, если она не принадлежит ребру
паросочетания. На рис. 12.1 слева
показан граф
и в нем выделены ребра паросочетания 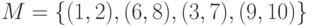 .
Вершины 4 и 5 - свободные. Заметим, что к этому
паросочетанию нельзя добавить ни одного
ребра, т.е. оно максимальное. Однако оно не является наибольшим. В этом
легко убедиться, если рассмотреть путь
.
Вершины 4 и 5 - свободные. Заметим, что к этому
паросочетанию нельзя добавить ни одного
ребра, т.е. оно максимальное. Однако оно не является наибольшим. В этом
легко убедиться, если рассмотреть путь 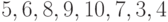 (показан
пунктиром). Он начинается и заканчивается в свободных вершинах, а вдоль
пути чередуются сильные и слабые ребра. Если на этом пути превратить
каждое сильное ребро в слабое, а каждое слабое - в сильное, то получится
новое паросочетание, показанное на рисунке справа, в котором на одно ребро
больше. Увеличение паросочетания с помощью подобных преобразований -
в этом и состоит суть метода увеличивающих путей.
(показан
пунктиром). Он начинается и заканчивается в свободных вершинах, а вдоль
пути чередуются сильные и слабые ребра. Если на этом пути превратить
каждое сильное ребро в слабое, а каждое слабое - в сильное, то получится
новое паросочетание, показанное на рисунке справа, в котором на одно ребро
больше. Увеличение паросочетания с помощью подобных преобразований -
в этом и состоит суть метода увеличивающих путей.
Сформулируем необходимые понятия и докажем теорему, лежащую в основе этого
метода. Чередующимся
путем относительно данного паросочетания
называется простой путь, в котором чередуются сильные и слабые ребра
(т.е. за сильным ребром следует слабое,
за слабым - сильное). Чередующийся путь
называется увеличивающим,
если он соединяет две свободные вершины.
Если  - паросочетание,
- паросочетание,  -
увеличивающий путь
относительно
-
увеличивающий путь
относительно  , то легко видеть, что
, то легко видеть, что  - тоже
паросочетание и
- тоже
паросочетание и  .
.
Теорема 2. Паросочетание является наибольшим тогда и только тогда, когда относительно него нет увеличивающих путей.
Доказательство. Если есть увеличивающий путь, то, поступая так, как
в рассмотренном примере,
то есть заменяя вдоль этого пути сильные ребра на
слабые и наоборот, мы, очевидно, получим большее паросочетание. Для
доказательства обратного утверждения рассмотрим паросочетание  в графе
в графе  и предположим, что
и предположим, что  - не
наибольшее. Покажем, что
тогда имеется увеличивающий путь относительно
- не
наибольшее. Покажем, что
тогда имеется увеличивающий путь относительно  .
Пусть
.
Пусть 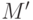 -
другое паросочетание и
-
другое паросочетание и 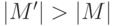 . Рассмотрим
подграф
. Рассмотрим
подграф  графа
графа  ,
образованный теми ребрами, которые входят в одно и только в одно
из паросочетаний
,
образованный теми ребрами, которые входят в одно и только в одно
из паросочетаний 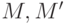 . Иначе говоря, множеством ребер
графа
. Иначе говоря, множеством ребер
графа  является симметрическая разность
является симметрическая разность  .
В графе
.
В графе  каждая вершина инцидентна не более чем двум
ребрам (одному из
каждая вершина инцидентна не более чем двум
ребрам (одному из  и одному из
и одному из 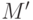 ), т.е. имеет
степень
не более двух. В таком графе каждая
компонента связности - путь или цикл. В каждом из этих путей и циклов
чередуются ребра из
), т.е. имеет
степень
не более двух. В таком графе каждая
компонента связности - путь или цикл. В каждом из этих путей и циклов
чередуются ребра из  и
и 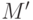 . Так
как
. Так
как 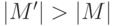 , имеется
компонента, в которой ребер из
, имеется
компонента, в которой ребер из 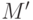 содержится больше, чем ребер
из
содержится больше, чем ребер
из  . Это может быть только путь, у которого оба концевых ребра
принадлежат
. Это может быть только путь, у которого оба концевых ребра
принадлежат 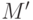 . Легко видеть, что относительно
. Легко видеть, что относительно  этот путь будет увеличивающим.
этот путь будет увеличивающим.
Для решения задачи о паросочетании остается научиться находить увеличивающие пути или убеждаться, что таких путей нет. Тогда, начиная с любого паросочетания (можно и с пустого множества ребер), можем строить паросочетания со все увеличивающимся количеством ребер до тех пор, пока не получим такое, относительно которого нет увеличивающих путей. Оно и будет наибольшим. Известны эффективные алгоритмы, которые ищут увеличивающие пути для произвольных графов. Рассмотрим сначала более простой алгоритм, решающий эту задачу для двудольных графов.

