|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Блоки
Блоки
Если граф состоит из нескольких компонент связности, то его можно изучать
"по частям", и это может упростить описание графа и облегчить
решение
многих задач. Однако и связный граф иногда можно представить как состоящий
из частей, и такое представление также может быть полезным. После
компонент связности простейшими частями такого рода являются блоки
(называемые также компонентами двусвязности). Блок - это максимальный
подграф графа, не имеющий собственных шарниров (т.е. некоторые шарниры
графа могут принадлежать блоку, но своих шарниров у блока нет).
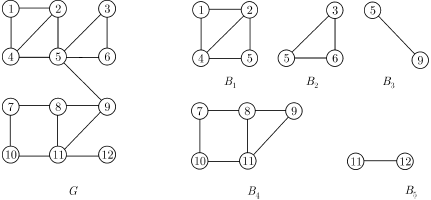
На рис. 6.1 изображены граф  и его блоки
и его блоки  . Ниже будет дано
другое определение блока, из которого ясно, почему блоки называют
компонентами двусвязности. Затем будут рассмотрены некоторые свойства
блоков и описан алгоритм выявления блоков, основанный на поиске в глубину.
. Ниже будет дано
другое определение блока, из которого ясно, почему блоки называют
компонентами двусвязности. Затем будут рассмотрены некоторые свойства
блоков и описан алгоритм выявления блоков, основанный на поиске в глубину.
Двусвязность
Связный граф с не менее чем тремя вершинами, в котором нет шарниров,
называется двусвязным. Примеры
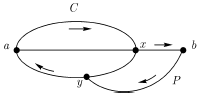
двусвязных графов - цикл 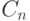 и полный граф
и полный граф 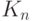 ,
,  цепь
же
цепь
же 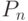 не является двусвязным графом ни при
каком
не является двусвязным графом ни при
каком  .
.
Будем говорить, что два элемента графа (напомним, что элементы графа - это вершины и ребра) циклически связаны, если в графе имеется простой цикл, содержащий оба эти элемента.
Теорема 1. В двусвязном графе любые два различных элемента циклически связаны. Если в графе любые два ребра циклически связаны, то он двусвязен.
Доказательство. Докажем сначала, что в двусвязном графе  для любых двух различных вершин
для любых двух различных вершин  и
и  имеется
простой
цикл, проходящий через обе эти вершины. Доказательство проводим индукцией
по расстоянию между
имеется
простой
цикл, проходящий через обе эти вершины. Доказательство проводим индукцией
по расстоянию между  и
и  . Если
. Если 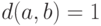 , то
, то  и
и  смежны.
Ребро
смежны.
Ребро 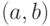 не является перешейком (иначе хотя бы одна
из вершин
не является перешейком (иначе хотя бы одна
из вершин  ,
,  была
бы шарниром). Но тогда в графе имеется простой цикл, проходящий через это
ребро. Пусть
была
бы шарниром). Но тогда в графе имеется простой цикл, проходящий через это
ребро. Пусть  . Рассмотрим кратчайший путь из
. Рассмотрим кратчайший путь из  в
в  , и пусть
, и пусть  - предпоследняя вершина этого
пути. Тогда
- предпоследняя вершина этого
пути. Тогда 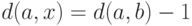 и, по
предположению индукции, существует простой цикл
и, по
предположению индукции, существует простой цикл  , содержащий
вершины
, содержащий
вершины  и
и  . Так как вершина
. Так как вершина  - не шарнир,
то существует простой путь
- не шарнир,
то существует простой путь  из
из  в
в  ,
не проходящий через
,
не проходящий через  . Пусть
. Пусть  - первая
вершина этого пути,
принадлежащая
- первая
вершина этого пути,
принадлежащая  (такая существует, так как
(такая существует, так как 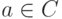 .
Тогда отрезок пути
.
Тогда отрезок пути  от
от  до
до  вместе
с отрезком
цикла от
вместе
с отрезком
цикла от  до
до  , содержащим вершину
, содержащим вершину  ,
и с ребром
,
и с ребром 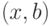 образует простой цикл, содержащий обе вершины
образует простой цикл, содержащий обе вершины  и
и  (показан стрелками на рис. 6.2).
(показан стрелками на рис. 6.2).
Теперь покажем, что для любой вершины  и любого
ребра
и любого
ребра 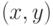 двусвязного графа
двусвязного графа  в нем имеется цикл, содержащий эту
вершину и это ребро. Как доказано выше, существует простой
цикл
в нем имеется цикл, содержащий эту
вершину и это ребро. Как доказано выше, существует простой
цикл 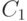 ,
содержащий вершины
,
содержащий вершины  и
и  . Если этот цикл проходит и
через
. Если этот цикл проходит и
через  ,
то, заменив в нем отрезок от
,
то, заменив в нем отрезок от  до
до  , не
содержащий
, не
содержащий  , ребром
, ребром 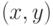 , получим простой цикл,
проходящий через
вершину
, получим простой цикл,
проходящий через
вершину  и ребро
и ребро 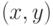 . В противном случае
возьмем цикл
. В противном случае
возьмем цикл 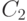 ,
содержащий вершины
,
содержащий вершины  и
и  . Кратчайший отрезок этого
цикла,
соединяющий
. Кратчайший отрезок этого
цикла,
соединяющий  с какой-либо вершиной
с какой-либо вершиной  на
на 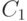 ,
вместе с отрезком цикла
,
вместе с отрезком цикла 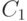 от
от  до
до  ,
содержащим
вершину
,
содержащим
вершину  , и с ребром
, и с ребром 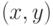 образует простой цикл,
содержащий это
ребро и вершину
образует простой цикл,
содержащий это
ребро и вершину  .
.
Доказательство того, что в двусвязном графе через любые два ребра проходит
простой цикл, почти в точности повторяет предыдущее, только вместо
вершины  нужно рассматривать ребро
нужно рассматривать ребро 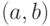 .
.
Остается доказать, что если в графе  через любые два
различных
элемента проходит простой цикл, то этот граф - двусвязный. Действительно,
допустим, что вершина
через любые два
различных
элемента проходит простой цикл, то этот граф - двусвязный. Действительно,
допустим, что вершина  - шарнир графа
- шарнир графа  .
Возьмем вершины
.
Возьмем вершины  и
и  , смежные с
, смежные с  и принадлежащие разным
компонентам связности графа, получающегося при удалении вершины
и принадлежащие разным
компонентам связности графа, получающегося при удалении вершины  .
Тогда в
.
Тогда в  не существует цикла, содержащего оба ребра
не существует цикла, содержащего оба ребра 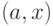 и
и 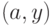 .
.
Из этой теоремы следует, что свойство двусвязности можно охарактеризовать следующим образом:
Следствие. Граф с не менее чем двумя ребрами двусвязен тогда и только тогда, когда в нем любые два различных ребра циклически связаны.
Рассмотрим подробнее отношение циклической связанности ребер. Оно, очевидно, симметрично. Будем считать, что каждое ребро циклически связано с самим собой, тогда это отношение будет и рефлексивным. Докажем, что оно на самом деле является отношением эквивалентности.
Теорема 2. Для любого графа отношение циклической связанности ребер является отношением эквивалентности.
Доказательство. Остается доказать транзитивность этого отношения.
Пусть 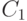 - простой цикл, содержащий
ребра
- простой цикл, содержащий
ребра 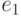 и
и 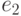 , а
, а 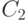 - простой цикл, содержащий
ребра
- простой цикл, содержащий
ребра 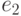 и
и 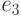 ; покажем, что существует простой цикл, содержащий ребра
; покажем, что существует простой цикл, содержащий ребра 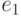 и
и 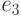 . Если
. Если 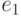 принадлежит
принадлежит 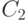 , то
последний и является этим циклом. Если же
, то
последний и является этим циклом. Если же 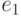 не принадлежит
не принадлежит 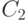 , то в
, то в 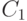 есть отрезок
есть отрезок 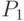 ,
включающий
,
включающий 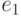 ,
у которого концевые вершины
,
у которого концевые вершины  и
и  принадлежат
принадлежат 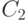 ,
а все внутренние вершины не принадлежат
,
а все внутренние вершины не принадлежат 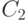 .
Пусть
.
Пусть 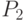 -
отрезок цикла
-
отрезок цикла 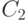 , концами которого являются
, концами которого являются  и
и  и который включает ребро
и который включает ребро 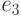 .
Соединение
.
Соединение 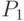 и
и 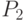 дает простой цикл, содержащий
дает простой цикл, содержащий 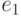 и
и 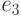 .
.
Итак, множество ребер любого графа разбивается на классы эквивалентности по отношению циклической связанности. Каждый перешеек образует отдельный класс эквивалентности. Если граф двусвязен, то имеется единственный класс циклической связанности.