|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Паросочетания
Паросочетания в двудольных графах
Пусть 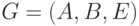 - двудольный граф c долями
- двудольный граф c долями  и
и  ,
,  - паросочетание в
- паросочетание в  . Всякий увеличивающий
путь, если
такой имеется, соединяет вершину из множества
. Всякий увеличивающий
путь, если
такой имеется, соединяет вершину из множества  с вершиной из множества
с вершиной из множества  .
.
Зафиксируем некоторую свободную вершину 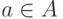 . Мы хотим найти
увеличивающий путь, начинающийся в
. Мы хотим найти
увеличивающий путь, начинающийся в  , либо убедиться в том, что
таких путей нет. Оказывается, нет необходимости рассматривать все
чередующиеся пути, начинающиеся в вершине
, либо убедиться в том, что
таких путей нет. Оказывается, нет необходимости рассматривать все
чередующиеся пути, начинающиеся в вершине  , для того, чтобы
установить, какие вершины достижимы из вершины
, для того, чтобы
установить, какие вершины достижимы из вершины  чередующимися
путями.
чередующимися
путями.
Вершину  назовем четной или нечетной в зависимости от
того, четно или нечетно расстояние между нею и вершиной
назовем четной или нечетной в зависимости от
того, четно или нечетно расстояние между нею и вершиной  .
Поскольку граф двудольный, любой путь, соединяющий вершину
.
Поскольку граф двудольный, любой путь, соединяющий вершину  с четной (нечетной) вершиной, имеет четную (нечетную) длину. Поэтому
в чередующемся пути, ведущем из вершины
с четной (нечетной) вершиной, имеет четную (нечетную) длину. Поэтому
в чередующемся пути, ведущем из вершины  в четную (нечетную)
вершину, последнее ребро обязательно сильное (слабое).
в четную (нечетную)
вершину, последнее ребро обязательно сильное (слабое).
Определим дерево
достижимости как максимальное дерево
с корнем  , в котором каждый путь,
начинающийся в корне, является чередующимся.
Дерево достижимости определено не однозначно, но любое такое дерево
в двудольном графе обладает следующим свойством:
, в котором каждый путь,
начинающийся в корне, является чередующимся.
Дерево достижимости определено не однозначно, но любое такое дерево
в двудольном графе обладает следующим свойством:
Лемма 1. Вершина  принадлежит дереву
достижимости тогда и только тогда, когда существует чередующийся путь,
соединяющий вершины
принадлежит дереву
достижимости тогда и только тогда, когда существует чередующийся путь,
соединяющий вершины  и
и  .
.
Доказательство. Рассмотрим некоторое дерево достижимости  и докажем, что всякая вершина
и докажем, что всякая вершина  , достижимая из вершины
, достижимая из вершины  чередующимся путем, принадлежит этому дереву. Проведем индукцию по длине
кратчайшего чередующегося пути из
чередующимся путем, принадлежит этому дереву. Проведем индукцию по длине
кратчайшего чередующегося пути из  в
в  . Пусть
. Пусть  -
предпоследняя (т.е. предшествующая
-
предпоследняя (т.е. предшествующая  ) вершина такого пути.
По предположению индукции, вершина
) вершина такого пути.
По предположению индукции, вершина  принадлежит
дереву
принадлежит
дереву  .
Если она четная, то любой чередующийся путь из вершины
.
Если она четная, то любой чередующийся путь из вершины  в вершину
в вершину  заканчивается сильным ребром.
Следовательно, в дереве
заканчивается сильным ребром.
Следовательно, в дереве  вершину
вершину  c ее отцом
соединяет
сильное ребро, а ребро
c ее отцом
соединяет
сильное ребро, а ребро 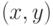 -
слабое. Поэтому, если добавить к дереву вершину
-
слабое. Поэтому, если добавить к дереву вершину  и ребро
и ребро 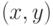 , то путь в дереве, соединяющий
, то путь в дереве, соединяющий  с
с  ,
будет чередующимся. Значит, если предположить, что дерево
,
будет чередующимся. Значит, если предположить, что дерево  не содержит вершины
не содержит вершины  , то окажется, что оно не
максимально, а это противоречит определению. Аналогично рассматривается
случай, когда вершина
, то окажется, что оно не
максимально, а это противоречит определению. Аналогично рассматривается
случай, когда вершина  - нечетная.
- нечетная.
Итак, для решения задачи остается научиться строить дерево достижимости.
Для этого можно использовать слегка модифицированный поиск в ширину из
вершины  . Отличие от стандартного поиска в ширину состоит в том,
что открываемые вершины делятся на четные и нечетные. Для четных вершин
исследуются инцидентные им слабые ребра, а для нечетных - сильные.
Через
. Отличие от стандартного поиска в ширину состоит в том,
что открываемые вершины делятся на четные и нечетные. Для четных вершин
исследуются инцидентные им слабые ребра, а для нечетных - сильные.
Через 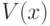 , как обычно, обозначается множество вершин, смежных
с вершиной
, как обычно, обозначается множество вершин, смежных
с вершиной  ,
,  - очередь, используемая при
поиске в ширину. Если
вершина
- очередь, используемая при
поиске в ширину. Если
вершина  не является свободной, т.е. инцидентна некоторому
сильному ребру, то другая вершина этого ребра обозначается
через
не является свободной, т.е. инцидентна некоторому
сильному ребру, то другая вершина этого ребра обозначается
через 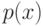 .
.
