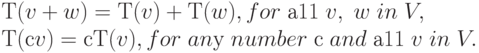| Россия, Сургут |
Линейные трансформации
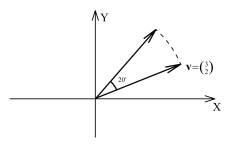
Рассмотрим следующую задачу: Возьмем вектор 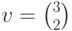 на плоскости ХУ и повернем его против часовой стрелки на
на плоскости ХУ и повернем его против часовой стрелки на 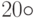 . Каковы будут координаты результирующего вектора
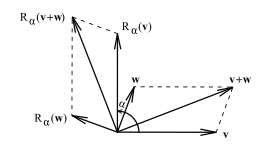
. Каковы будут координаты результирующего вектора  ? Нетрудно найти решение, используя геометрию треугольников, но есть лучший подход, основанный на теоретическом анализе свойств трансформации поворотов. Если у нас есть два вектора v и w, то не имеет значение, найдем ли мы раньше сумму этих векторов и повернем суммарный вектор на угол
? Нетрудно найти решение, используя геометрию треугольников, но есть лучший подход, основанный на теоретическом анализе свойств трансформации поворотов. Если у нас есть два вектора v и w, то не имеет значение, найдем ли мы раньше сумму этих векторов и повернем суммарный вектор на угол  или вначале повернем каждый из векторов v и w на угол
или вначале повернем каждый из векторов v и w на угол  , а затем найдем суммарный вектор. Окончательный результат будет один и тот же.
, а затем найдем суммарный вектор. Окончательный результат будет один и тот же.
Линейные трансформации - английский термин " Transformation" мы решили переводить как " Трансформация", а не как " Преобразование". Это позволяет подчеркнуть специфичность этот термина, играющего важный смысл в данном тексте. Термин " Преобразование" используется в других контекстах.
Это свойство поворотов алгебраически записывается следующим образом:
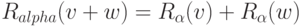
Это же свойство применимо и к результату умножения вектора на число для любого вещественного числа с:

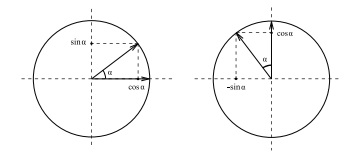
Заметим, что довольно просто вычислить результат трансформации, когда он применяется к базисным векторам 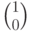 и
и 
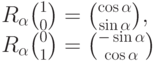
Теперь мы можем вычислить результат трансформации поворота, применимой к вектору 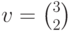 , записав его следующим образом:
, записав его следующим образом:
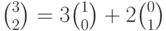
В результате получим:
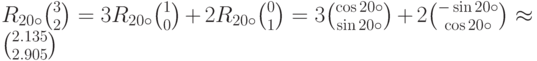
Теперь мы хотим применить идею такого способа вычислений в более общей ситуации.
Рассмотрим векторное пространство - множество векторов, для которых определена операция сложения векторов и операция умножения векторов на числа. Пусть эти операции удовлетворяют некоторому списку свойств. Мы не собираемся перечислять здесь свойства из этого списка, достаточно сказать, что все они являются естественными свойствами, соответствующие ожиданиям. Примером может служить свойство, применимое для любой пары векторов v, w и произвольного числа с: с(v + w) = сv + сw.
Примерами векторных пространств являются:
- Множество векторов на плоскости;
- Множество векторов трехмерного пространства;
- Множество n-кубитов.
Существует алгебраическая конструкция, которая унифицирует все приведенные выше примеры. Пространство 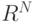 определяется как множество кортежей размера N, содержащих вещественные числа. Операции сложения векторов и умножения на число выполнятся над компонентами векторов:
определяется как множество кортежей размера N, содержащих вещественные числа. Операции сложения векторов и умножения на число выполнятся над компонентами векторов:
Философия, предложенная Рене Декартом, состоит в том, чтобы иметь две модели для векторов на плоскости: геометрическую модель, где вектора представляются направленными отрезками на плоскости, и алгебраическую, где вектора задаются парой чисел. Преимущество геометрической модели в том, что она допускает визуализацию, в то время как алгебраическая модель удобнее при проведении вычислений. Некоторые задачи проще решаются на геометрической модели, другие - на алгебраической.
Пространство 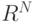 имеет базис
имеет базис  , где
, где
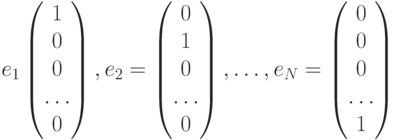
Каждый вектор в  может быть представлен в виде линейной комбинации базисных векторов:
может быть представлен в виде линейной комбинации базисных векторов:
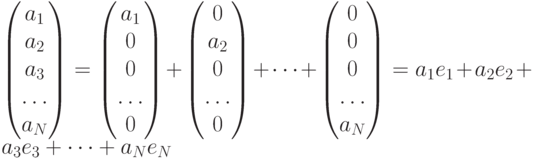
Сравнивая эту формулу с выражением для 2-кубита

можно заметить, что в пространстве 2-кубита базис содержит четыре чистые вектора состояний 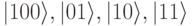 . Этот подход очевидным способом обобщается на пространство n-кубита.
. Этот подход очевидным способом обобщается на пространство n-кубита.
Размерность векторного пространства задается числом базисных векторов. Мы видели, что размерность пространства 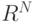 равна N. Размерность векторного пространства n-кубитов равна
равна N. Размерность векторного пространства n-кубитов равна 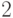 .
.
В дополнение к выше приведенным примерам конечномерных пространств следует упомянуть и пространства бесконечной размерности. Примером такого пространства является множество полиномов от одной переменной Х. Также, как и для векторов на плоскости, здесь определена операция сложения полиномов и операция умножения полинома на число. Что является базисом в пространстве полиномов? Полином записывается следующим образом: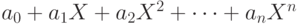 .
.
Мы видим, что коэффициенты 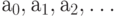 можно интерпретировать как координаты вектора,
можно интерпретировать как координаты вектора, 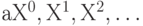 как базис в пространстве полиномов. Так как степеней полинома может быть бесконечно много, то и пространство полиномов является бесконечномерным.
как базис в пространстве полиномов. Так как степеней полинома может быть бесконечно много, то и пространство полиномов является бесконечномерным.
Определение. Трансформация Т векторного пространства V называется линейной, если она удовлетворяет следующим двум свойствам: