| Россия, Сургут |
Теорема Лагранжа
Случается, что внутри группы есть еще одна группа меньшего размера. Например, внутри диедральной группы 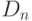 множество поворотов
множество поворотов 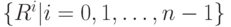 является группой. Это пример подгруппы.
является группой. Это пример подгруппы.
Определение. Пусть G - группа. Подмножество Н в G называется подгруппой, если вьшолняются следующие свойства:
- е принадлежит Н;
- Для каждого элемента h из Н его обратный элемент
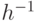 также содержится в Н;
также содержится в Н; - Для любой пары элементов
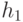 и
и 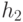 из Н их произведение
из Н их произведение 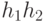 также содержится в Н.
также содержится в Н.
Можно видеть, что множество положительных рациональных чисел 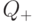 представляет подгруппу мультипликативной группы
представляет подгруппу мультипликативной группы 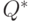 , четные целые числа представляют подгруппу в аддитивной группе Z. Еще одним примером подгруппы является множество {е, Т} в
, четные целые числа представляют подгруппу в аддитивной группе Z. Еще одним примером подгруппы является множество {е, Т} в 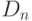 . Множество из одного элемента {е} и само множество G также являются подгруппами для любой группы G.
. Множество из одного элемента {е} и само множество G также являются подгруппами для любой группы G.
Множество ортогональных матриц размера N*N формирует подгруппу, обозначаемую О(N), в обобщенной линейной группе GL(N).
Упражнение. Определить все возможные подгруппы в  .
.
Важным классом подгрупп являются циклические подгруппы. Зафиксируем элемент g в группе G. Пусть Н будет множеством всех целых степеней g:
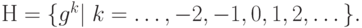
Ясно, что это множество является подгруппой, так как  Если группа G конечна, то циклическая подгруппа, генерируемая элементом g не может быть бесконечной и список степеней g будет содержать бесконечно много повторений. Давайте проанализируем структуру подгруппы в этом случае.
Если группа G конечна, то циклическая подгруппа, генерируемая элементом g не может быть бесконечной и список степеней g будет содержать бесконечно много повторений. Давайте проанализируем структуру подгруппы в этом случае.
Определение. Порядком элемента g в группе G является наименьшее натуральное число n, такое что 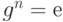 . Если такового числа не существует, то значение порядка - бесконечность.
. Если такового числа не существует, то значение порядка - бесконечность.
Примеры. В группе  элемент Т имеет порядок 2, а элемент R - 4. В
элемент Т имеет порядок 2, а элемент R - 4. В 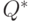 элемент g = -1 имеет порядок 2, так как
элемент g = -1 имеет порядок 2, так как 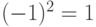 , а элемент g = 5 имеет бесконечный порядок, так как никакая положительная степень числа 5 не дает 1.
, а элемент g = 5 имеет бесконечный порядок, так как никакая положительная степень числа 5 не дает 1.
Утверждение. Пусть G - конечная группа. Тогда любой элемент g в G имеет конечный порядок. Если n - порядок g, то циклическая подгруппа, генерируемая g имеет n элементов: 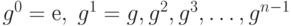
Доказательство. Так как множество всех степеней должно содержать повторения, то имеет место  для некоторых целых
для некоторых целых  . Умножая обе части равенства на
. Умножая обе части равенства на 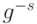 , получим:
, получим: 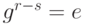 , где r - s - положительное число. Следовательно, g - конечная группа.
, где r - s - положительное число. Следовательно, g - конечная группа.
Пусть n - порядок G. Тогда 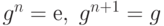 , и так далее. Каждая положительная степень g приводится к одному из элементов:
, и так далее. Каждая положительная степень g приводится к одному из элементов:  Для отрицательных степеней g справедливо
Для отрицательных степеней g справедливо 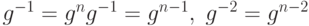 , и так далее. Из этого следует справедливость нашего утверждения.
, и так далее. Из этого следует справедливость нашего утверждения.
Определение. Группа G называется циклической, если существует элемент g в G, такой что целые степени g исчерпывают G.
Определение. Пусть g - элемент группы G и пусть Н - подгруппа в G. Смежный класс (coset) gH - это множество произведений gh, где h пробегает все значения из Н.
Давайте рассмотрим смежные классы подгруппы 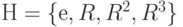 в диедральной группе
в диедральной группе  .
.
Очевидно, что смежный класс еН совпадает с Н. Смежный класс RH также совпадает с Н, поскольку он содержит элементы 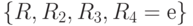 . Смежный класс
. Смежный класс 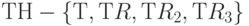 . Фактически для любого I смежные классы
. Фактически для любого I смежные классы 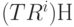 и смежный класс ТН совпадают. В данном примере можно видеть, что есть только два различных смежных классы:
и смежный класс ТН совпадают. В данном примере можно видеть, что есть только два различных смежных классы:  и
и  .
.
Из принципа Судоку для таблицы умножения следует, что размер любого смежного класса gH равен числу элементов в подгруппе Н.
Утверждение. Пусть Н - подгруппа в группе G. Тогда G - это объединение неперекрывающихся смежных классов.
Доказательство. Необходимо показать, что два различных смежных класса не перекрываются, это значит, что если два смежных класса аН и bН имеют общий элемент с, то классы эквивалентны. В самом деле, если с принадлежит обоим классам, то 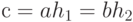 для некоторых
для некоторых 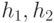 в Н. Тогда
в Н. Тогда 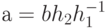 . Нам нужно показать, что любой элемент аН содержится в bН и наоборот. Пусть d - элемент аН. Тогда для некоторого
. Нам нужно показать, что любой элемент аН содержится в bН и наоборот. Пусть d - элемент аН. Тогда для некоторого 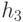 в Н,
в Н, 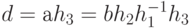 . Так как Н - подгруппа, то
. Так как Н - подгруппа, то 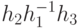 содержится в Н, следовательно, d принадлежит смежному классу bН. Аналогично, каждый элемент bН содержится в классе аН, так что аН = bН.
содержится в Н, следовательно, d принадлежит смежному классу bН. Аналогично, каждый элемент bН содержится в классе аН, так что аН = bН.
Смежные классы покрывают всю группу, поскольку каждый элемент g принадлежит своему собственному смежному классу gН.
Определение. Число элементов группы G называется порядком группы.
Теорема (Лагранжа). Пусть G - конечная группа.
(а) Порядок любой подгруппы Н в G является делителем порядка G
(b) Порядок любого элемента g в G является делителем порядка G.
Доказательство. Группа G является объединением неперекрывающихся смежных классов подгруппы Н. Поскольку все классы имеют один и тот же размер, то:
Порядок G = Порядок Н * Число смежных классов Н.
Из этого следует справедливость утверждения части (а) нашей теоремы.
Для доказательства части (b) заметим, что каждый элемент g генерирует циклическую подгруппу, чей порядок эквивалентен порядку элемента g, а это значит, что (b) следует из (а).
Следствие. Пусть G - группа порядка n и пусть g - элемент G. Тогда 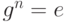 .
.
Доказательство. Пусть k - порядок g. По теореме Лагранжа n = ks для некоторого s. Тогда