| Россия, Сургут |
Классические вычисления на квантовом компьютере
Любое классическое вычисление может рассматриваться как функция, на входе у которой строка битов длины n, а на выходе строка битов длины k:
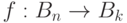
Множество бинарных строк длины n обозначаем как 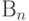 .
.
В качестве простого примера рассмотрим функцию, которая вычисляет квадрат двоичного целого длиной 3 бита, 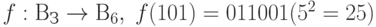 . Нам необходим результат длиной 6 битов, поскольку для входа 111 функция f дает результат длиной б битов -110001.
. Нам необходим результат длиной 6 битов, поскольку для входа 111 функция f дает результат длиной б битов -110001.
Эта интерпретация справедлива не только для функций арифметической природы, но применима к любым компьютерным программам. Каковы бы не были данные, с которыми работает программа, в памяти компьютера эти данные хранятся как строки битов и все вычисления дают в результате строку битов. Поэтому любая компьютерная программа имеет на входе фактически строку битов и получает результат также в виде строки битов. Так что без потери общности классическое вычисление по компьютерной программе можно рассматривать как функцию 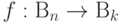 .
.
Хотелось бы понять, как можно классическое вычисление закодировать на квантовом компьютере. Первый барьер, который необходимо преодолеть на этом пути, состоит в том, что квантовый алгоритм обратим, а функции классического алгоритма таким свойством не обладают.
Давайте классическую функцию 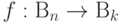 , преобразуем в обратимую функцию:
, преобразуем в обратимую функцию:
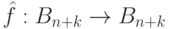
Мы хотим вход и выход объединить в одну строку, так что вход и выход будут принадлежать одному множеству, при этом начальные биты, соответствующие входу х не меняются в ходе вычислений, а биты результата на входе имеют значение 0, а в результате вычислений получают значение f (х). Формально:
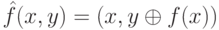
Здесь х - n-битный вход, y - начальное значение выходных битов, а символом  обозначена операция побитового сложения по модулю 2.
обозначена операция побитового сложения по модулю 2.
При использовании 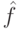 в приложениях выходные биты у всегда инициализируются нулевой строкой. Тогда мы можем использовать
в приложениях выходные биты у всегда инициализируются нулевой строкой. Тогда мы можем использовать 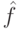 для вычисления f:
для вычисления f:
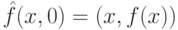
Заметьте, 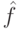 не изменяет значений входных битов.
не изменяет значений входных битов.
Например, если 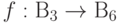 - функция, которая вычисляет квадрат 3-битного целого, то
- функция, которая вычисляет квадрат 3-битного целого, то

В записи строки битов запятая между х и у ставится только для удобства чтения, х и у - это две части единой строки битов. Хотя нас интересуют вычисления, где у инициализируется нулевой строкой, функция 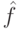 определена для всех 9-битных аргументов, например,
определена для всех 9-битных аргументов, например,

Чтобы вычислить значение последних 6-и битов, мы вначале вычисляем значение функции f (101) = 011001, а затем выполняем побитовое сложение по модулю 2 результата функции и начального состояния выходных битов:

Утверждение. Пусть f- некоторое классическое вычисление  ,. Тогда функция
,. Тогда функция  , определенная как
, определенная как
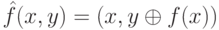
обратима. Обратной к 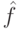 функции является сама функция
функции является сама функция 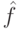 .
.
Доказательство. Необходимо доказать, что 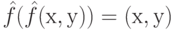 . В самом деле,
. В самом деле,

В доказательстве использованы свойства побитового сложения по модулю 2- сложение строки с самой строкой дает нулевую строку, а сложение у с нулевой строкой сохраняет у.
Пришла пора напомнить, что квантовые вычисления представляют ортогональную линейную трансформацию на пространстве n-кубитов. Поэтому необходимо обратимую классическую функцию представить в виде линейной трансформации. Для определения трансформации необходимо задать значения базисных векторов, а базис в пространстве п-кубитов задается бинарными строками длины n.
С классической функцией 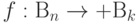 , мы связываем линейную трансформацию
, мы связываем линейную трансформацию 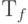 в пространстве (n + k)-кубитов, определенную как:
в пространстве (n + k)-кубитов, определенную как:

Заметьте, 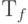 - трансформация весьма специального вида - она преобразует каждый базисный вектор в другой базисный вектор. Типично для квантовых вычислений линейная трансформация преобразует базисный вектор в линейную комбинацию базисных векторов._
- трансформация весьма специального вида - она преобразует каждый базисный вектор в другой базисный вектор. Типично для квантовых вычислений линейная трансформация преобразует базисный вектор в линейную комбинацию базисных векторов._
Трансформация 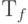 обратима, поскольку
обратима, поскольку 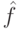 обратима. Более того,
обратима. Более того,  .
.
Так как 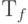 переставляет вектора в базисе, то образы этих векторов ортогональны друг другу и все имеют единичную длину, следовательно,
переставляет вектора в базисе, то образы этих векторов ортогональны друг другу и все имеют единичную длину, следовательно, 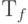 -ортогональная линейная трансформация.
-ортогональная линейная трансформация.
Например, для ранее рассмотренной функции 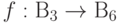 трансформация
трансформация 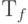 - это линейная трансформация на 512-мерном пространстве 9-кубитов, которая может быть задана матрицей размера 512 х 512 (по понятным причинам выписывать эту матрицу мы не будем). Так как
- это линейная трансформация на 512-мерном пространстве 9-кубитов, которая может быть задана матрицей размера 512 х 512 (по понятным причинам выписывать эту матрицу мы не будем). Так как 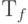 переставляет базисные вектора, то эта матрица в каждой строке и в каждом столбце имеет ровно одну единицу
переставляет базисные вектора, то эта матрица в каждой строке и в каждом столбце имеет ровно одну единицу
Определение 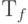 показывает возможность реализации классических вычислений на квантовом компьютере. Естественно, квантовый компьютер способен делать больше, чем просто моделировать классические вычисления. После всего, мы для достижения цели использовали только матрицы перестановок, а в нашем распоряжения имеются матрицы разного вида. Все же появляется одно новое свойство при выполнении классических вычислений на квантовом компьютере. Представьте себе, что мы в`качестве входа к
показывает возможность реализации классических вычислений на квантовом компьютере. Естественно, квантовый компьютер способен делать больше, чем просто моделировать классические вычисления. После всего, мы для достижения цели использовали только матрицы перестановок, а в нашем распоряжения имеются матрицы разного вида. Все же появляется одно новое свойство при выполнении классических вычислений на квантовом компьютере. Представьте себе, что мы в`качестве входа к 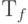 используем состояние
используем состояние
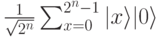
В этой записи х - n-битное целое число, а 0 представляет строку из k нулей. Множитель нормирует вектор, делая его длину, равную единице.
Мы получим
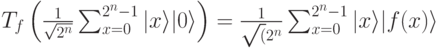
Теперь новое состояние содержит информацию о всех значениях f (х) для всех возможных х. Для достижения подобного эффекта на классическом компьютере нам пришлось бы вычислять значения f (х) последовательно, и мы были бы вынуждены выполнять 2n итераций. Это было бы недопустимо долго даже для скромных значений n (после всего возраст вселенной оценивается менее чем 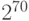 миллисекунд).
миллисекунд).
Квантовый компьютер вычислит все за одну итерацию. Это произойдет, поскольку мы организовали вход как суперпозицию всех возможных классических входов (это предполагает запутывание). Тогда квантовое вычисление, будучи линейной трансформацией, получит выход как суперпозицию всех возможных значений f (х). Это показывает, что квантовые вычисления массивно параллельны.
Недостаток лишь в том, что из выходного состояния невозможно извлечь информацию о каждом значении f . Представьте себе, что мы хотим найти решение уравнения f (х) = 0 и для простоты будем полагать, что уравнение имеет единственное решение х = а. Тогда нам хотелось бы знать какой из термов выхода имеет значение 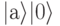 . Но мы не можем получить значение " а" путем измерений. Если мы выполним измерение, то будем наблюдать значение
. Но мы не можем получить значение " а" путем измерений. Если мы выполним измерение, то будем наблюдать значение 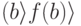 для случайного входа b.
для случайного входа b.
Вызов, стоящий перед нами, в том, чтобы при проектировании квантовых алгоритмов научиться так организовывать вычисления, чтобы получать правильный ответ, дающий решение нашей задачи, с высокой степенью вероятности.
