Линейные трансформации

Поворот на плоскости представляет пример линейной трансформации. Другими примерами являются отражение плоскости относительно прямой, проходящей через начало координат, и растяжение плоскости с фиксированным коэффициентом растяжения.

Ключевое свойство линейной трансформации в том, что она полностью определяется трансформациями базисных векторов. Предположим, что Т -линейная трансформация в и нам известны трансформации базисных векторов 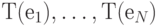. Тогда для произвольного вектора

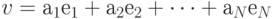
трансформация вектора вычисляется так:

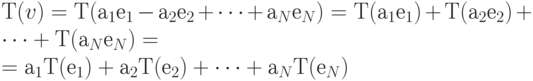
Этот метод мы использовали при вычислении образа вектора 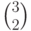для трансформации поворота вектора.

Еще один пример для тех, кто знаком с дифференциальным исчислением. Давайте рассмотрим трансформацию D в пространстве полиномов, где каждый полином f (Х) трансформируется в свою производную: 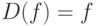. Линейные свойства трансформации D представляют известные правила дифференцирования для суммы переменных и умножения переменной на константу:

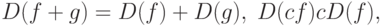
Следовательно, взятие производной можно рассматривать как линейную трансформацию. Из правил дифференцирования следуют трансформации базисных векторов в пространстве полиномов . Нетрудно видеть, что взятие производной для полинома выполняется в полном соответствии с нашим подходом к трансформациям - полином представляется в виде комбинации базисных векторов, а его производная вычисляется, используя линейные свойства трансформации, например,

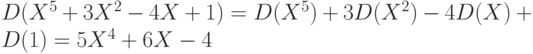
Давайте теперь обсудим приложение теории линейных трансформаций к квантовой криптографии. Вспомним, что в схеме получения секретного потока ключей Алиса и Боб получают фотоны, формирующие запутанные пары. Каждая пара в находится в состоянии 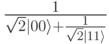. Когда они вьшолняют измерения, то с вероятностью 0.5 они получают "0", с такой же вероятностью они могут получить " 1". Благодаря запутанности их результаты измерений будут совпадать.

Представим себе, что Ева пытается атаковать эту схему и способна заменить поток запутанных пар потоком незапутанных пар в случайно выбранных состояниях и . В этом случае Алиса и Боб по-прежнему будут иметь согласованные результаты измерений и в примерно половине случаев результаты будут равны 0, а в остальных -1. Так как эти состояния сгенерированы Евой, то Ева будет знать результаты наблюдений Боба и Алисы и, следовательно, будет знать секретный ключ.

Как могут Алиса и Боб обнаружить атаку Евы? Предположим, что Алиса и Боб оба вращают свои поляризационные фильтры на один и тот же угол У. Можно ли предсказать результаты измерений? Математически это эквивалентно применению трансформации поворота каждого кубита, а затем проведению измерений. Квантовые состояния фотонов трансформируются следующим образом:

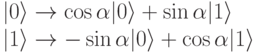
Так как одна и та же трансформация применима к первому и второму фотону пары, в результате получим:

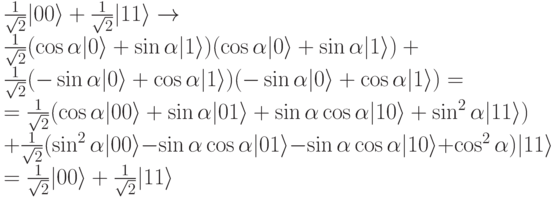
Мы пришли к неожиданному результату - после выполнения поворота запутанное состояние не изменилось! Это означает, что после поворота их поляризационных фильтров приходим к одним и тем же новым осям, так что не будет никаких изменений в статистике наблюдений. Алиса и Боб по-прежнему будут одновременно наблюдать нули и единицы со 100% корреляцией.

Теперь давайте посмотрим, что произойдет при получении Алисой и Бобом фотонов, посланных Евой, в незапутанном состоянии:

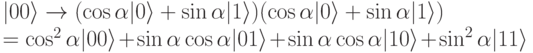
Мы видим, что в этом случае для некоторых наблюдений Алиса может получить 1, в то время как Боб будет наблюдать 0. Достаточно просто вычислить вероятность такой ситуации как функцию угла .

Для проверки целостности канала Алисе и Бобу достаточно измерить часть их потока с различным выравниванием поляризационных фильтров. Затем они могут обменяться результатами измерений по открытому каналу 100% совпадение результатов указывает на отсутствие атаки. Естественно, что биты, используемые для тестирования, не должны использоваться при генерации секретного ключа.

В заключение этой главы поясним идею параллелизма в квантовых вычислениях. Здесь мы сформулируем лишь саму идею в упрощенной форме, детали появятся последующих лекциях. Как уже упоминалось в лекции о квантовой механике, квантовый алгоритм представляет линейную трансформацию состояний в пространстве n-кубитов. Предположим, что мы хотим получить значения функции f (х) для 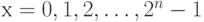. Предположим еще, что значения этой функции - это целые числа из n битов. Мы можем определить линейную трансформацию F в пространстве п-кубитов, которая трансформирует базисный вектор 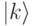в другой базисный вектор 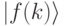. Тогда начальное состояние:

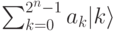
квантовый алгоритм F преобразует в состояние:

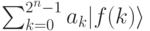
Мы видим, что при выполнении квантового алгоритма появляется возможность получить состояние, включающее все 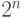значений функции f . Заметьте, что для классического компьютера цикл, содержащий 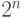итераций не может быть выполнен за сколь либо разумное время (например, время возраста вселенной) даже для относительно малых значений n, например, n = 100. Отсюда следует, что квантовый компьютер допускает "массивные" вычисления, аналогов которым нет в вычислениях на классических компьютерах.