|
мне задали дистанционное задание на сертификат,но я не могу его найти |
Вычисление оптимальных стратегий в бесконечных играх
Задача
Распределение атакующих единиц между двумя объектами ( Дрешер М. Стратегические игры. М., "Советское радио" ,1964.).
Предположим, что планируется атака двух населенных пунктов  и
и  , имеющих соответственно важности (ценности)
, имеющих соответственно важности (ценности) 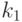 и
и 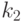 . Пусть противники, один из которых атакует (игрок I), а второй обороняется (игрок II), имеют по
. Пусть противники, один из которых атакует (игрок I), а второй обороняется (игрок II), имеют по  боевых единиц и пусть
боевых единиц и пусть  достаточно велико.
достаточно велико.
Эти единицы могут быть распределены следующим образом. Игрок I может выделить 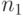 единиц для атаки объекта
единиц для атаки объекта  и
и  единиц для атаки объекта
единиц для атаки объекта  . В свою очередь игрок II может выделить
. В свою очередь игрок II может выделить 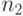 единиц для обороны объекта
единиц для обороны объекта  и
и  единиц для обороны объекта
единиц для обороны объекта  . При этом будем считать, что одна единица игрока II поражает только одну единицу игрока I.
. При этом будем считать, что одна единица игрока II поражает только одну единицу игрока I.
Допустим, что критерий эффективности игрока I пропорционален числу атакующих единиц, достигших объекта, и ценности объекта.
Обозначим
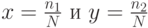 |
( 10.18) |
Тогда чистыми стратегиями игроков будут числа из интервала ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) вида (10.18.) Следовательно, необходимо решать матричную игру больших размеров. Однако, если N достаточно велико, можно полагать, что игрок I выбирает любое
вида (10.18.) Следовательно, необходимо решать матричную игру больших размеров. Однако, если N достаточно велико, можно полагать, что игрок I выбирает любое ![x\in [0,1]](/sites/default/files/tex_cache/c628ba2b1047de93f66cb815d986e107.png) , а игрок II — любое
, а игрок II — любое ![y\in [0,1]](/sites/default/files/tex_cache/ab3abad183cd9e117cb5711a60e1bc1d.png) .
.
Таким образом, первоначальная конфликтная ситуация хорошо моделируется бесконечной игрой на единичном квадрате с функцией выигрыша
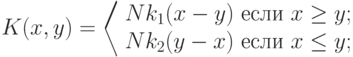 |
( 10.19) |
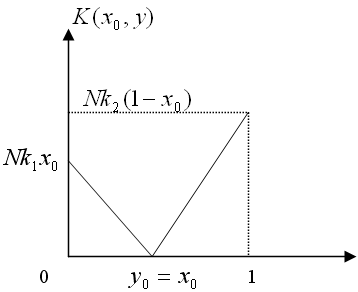
Путем построения графиков функции 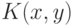 для фиксированных
для фиксированных  легко убедиться, что эта функция выпукла по
легко убедиться, что эта функция выпукла по  (рис. 10.6).
(рис. 10.6).
Следовательно,
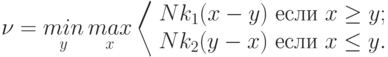
Из рассмотрения функции 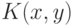 для различных фиксированных значений
для различных фиксированных значений 
можно убедиться, что если
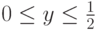 , то
, то
 ,
,
а если 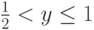 , то
, то
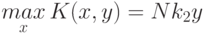 .
.
Отсюда
![\mathop{max}\limits_x K(x,y)=max[Nk_1(1-y),Nk_2y]](/sites/default/files/tex_cache/f5a67059731b1b54d507e88f99c04e0a.png) .
.
Итак,
![\nu=\mathop{min}\limits_y max[Nk_1(1-y),Nk_2y]](/sites/default/files/tex_cache/a3f3883bbe3408b5cb833d2bca34eb73.png) |
( 10.20) |
Из рассмотрения функции
![max[Nk_1(1-y),Nk_2y]](/sites/default/files/tex_cache/7c46c888667acb24c1a223dffdd310b9.png)
видно, что она принимает минимальное значение при 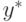 , которое удовлетворяет уравнению
, которое удовлетворяет уравнению
 |
( 10.21) |
Из уравнения (10.21.) находим
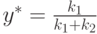 .
.
Тогда на основании (10.20.)
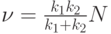 .
.
Следовательно, с учетом (10.18.) оптимальная стратегия игрока II состоит в выделении 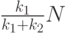 единиц для обороны объекта
единиц для обороны объекта  и
и 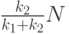 единиц для обороны объекта
единиц для обороны объекта  .
.
Для определения оптимальной стратегии игрока I воспользуемся теоремой 1.
Находим
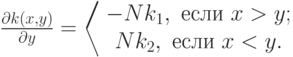
Составляем уравнение
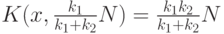 ,
,
то есть, если x\ge y, то
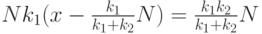 |
( 10.22) |
если  , то
, то
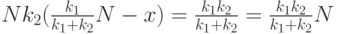 |
( 10.23) |
Уравнение (10.22.) имеет решение 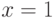 , а уравнение (10.23.) имеет решение
, а уравнение (10.23.) имеет решение 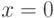 .
.
Так как
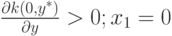
и
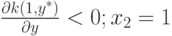 ,
,
то на основании теоремы(10.1.) игрок I имеет оптимальную стратегию вида
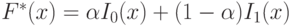 .
.
Для определения  составляем следующее уравнение:
составляем следующее уравнение:
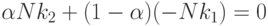 |
( 10.24) |
Уравнение (10.24.) имеет решение:
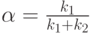 .
.
Таким образом, оптимальная стратегия игрока I заключается в том, чтобы нанести удар всеми силами по объекту  или
или  , руководствуясь случайным выбором, то есть выбирая объект
, руководствуясь случайным выбором, то есть выбирая объект  с вероятностью
с вероятностью 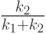 и
и  с вероятностью
с вероятностью 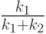 .
.
Итак, на основании решения рассмотренной игры получены рекомендации, согласно которым обороняющаяся сторона может свои силы распределить заранее вполне определенным образом – назначить 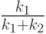 часть сил для обороны объекта
часть сил для обороны объекта  и
и 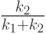 часть для обороны объекта
часть для обороны объекта  .
.
Нападающая сторона должна случайным образом сосредоточить все силы для атаки объекта  или
или  соответственно их важности.
соответственно их важности.
Например, если объект  в два раза важнее объекта
в два раза важнее объекта  , то объект
, то объект  должны оборонять
должны оборонять  всех имеющихся сил. В свою очередь, нападающая сторона должна атаковать этот объект всеми силами с вероятностью
всех имеющихся сил. В свою очередь, нападающая сторона должна атаковать этот объект всеми силами с вероятностью  .
.