|
мне задали дистанционное задание на сертификат,но я не могу его найти |
Вычисление оптимальных стратегий в бесконечных играх
Описание бесконечной игры
Общие методы вычисления оптимальных стратегий в бесконечных играх в настоящее время еще мало разработаны. Поэтому рассмотрим только некоторые частные игры, которые представляют практический интерес и допускают сравнительно простой подход при вычислении оптимальных стратегий (Абчук В.А., Емельянов Л.А., Матвейчук Ф.А., Суздаль В.Г. "Введение в теорию выработки решений" В. издательство, Москва, 1972.) .
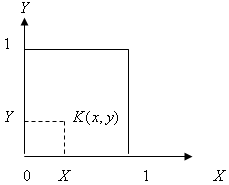
К бесконечным играм относятся модели конфликтных ситуаций, в которых каждая из противоположных сторон выбирает некоторые значения непрерывно меняющегося параметра (процентное соотношение распределения поисковых сил по районам поиска или бюджета между компаниями). В этом случае чистые стратегии игроков представляют выборы тех или иных чисел из некоторого интервала. Без потери общности можно считать, что эти стратегии являются точками отрезка единичной длины ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) . Тогда такую игру можно описать следующим образом.
. Тогда такую игру можно описать следующим образом.
Игрок I выбирает чистую стратегию  , где
, где  , а игрок II выбирает чистую стратегию
, а игрок II выбирает чистую стратегию  , где
, где 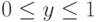 . Выбранные стратегии
. Выбранные стратегии  и
и  определяют ситуацию
определяют ситуацию 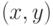 , в которой игрок I получает выигрыш
, в которой игрок I получает выигрыш 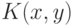 . Множество ситуаций заполняет единичный квадрат (рис. 10.1).
. Множество ситуаций заполняет единичный квадрат (рис. 10.1).
По этому иногда такие игры называют играми на единичном квадрате. Функция, ставящая в соответствие каждой ситуации выигрыш, который получает игрок I, называется функцией выигрыша.
Предположим, что функция 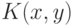 имеет минимум по
имеет минимум по  для
для 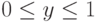 и максимум
и максимум  для
для 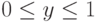 . Тогда, если игрок I выберет
. Тогда, если игрок I выберет  , то как бы ни действовал игрок II, первый может рассчитывать выиграть по меньшей мере
, то как бы ни действовал игрок II, первый может рассчитывать выиграть по меньшей мере
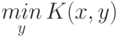 .
.
Поскольку игрок I может выбрать любое  из интервала
из интервала ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) , он может выбрать и такое
, он может выбрать и такое  , при котором его выигрыш будет максимальным, то есть игрок I при надлежащим выборе
, при котором его выигрыш будет максимальным, то есть игрок I при надлежащим выборе  гарантирует себе выигрыш не меньше чем
гарантирует себе выигрыш не меньше чем
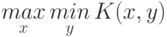 .
.
Аналогично игрок II может выбрать такое y, при котором игрок I не выиграет более чем
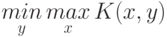 .
.
Следовательно, существует неравенство
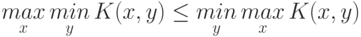 |
( 10.1) |
Если в (9.1.) имеет место равенство, то есть
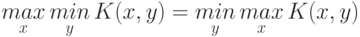 ,
,
то функция выигрыша 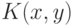 имеет седловую точку, то есть существуют такие
имеет седловую точку, то есть существуют такие  и
и  , при которых
, при которых 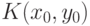 является одновременно минимальным по
является одновременно минимальным по  и максимальным по
и максимальным по  . Очевидно, что в этом случае
. Очевидно, что в этом случае
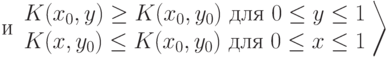 |
( 10.2) |
Если при любых  и
и  пара
пара 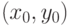 удовлетворяет неравенствам (2), то эта пара называется решением игры в чистых стратегиях. Соответственно этому игроки должны применять чистые стратегии
удовлетворяет неравенствам (2), то эта пара называется решением игры в чистых стратегиях. Соответственно этому игроки должны применять чистые стратегии  и
и  , которые называются оптимальными. При
, которые называются оптимальными. При

игроки должны применять смешанные стратегии.
Смешанная стратегия в бесконечной игре на единичном квадрате представляет собой случайный выбор числа из интервала ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) , то есть если задана смешанная стратегия, то это определяет закон распределения, в соответствии с которым игрок выбирает число из интервала
, то есть если задана смешанная стратегия, то это определяет закон распределения, в соответствии с которым игрок выбирает число из интервала ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) . Для математического описания такого закона распределения удобно пользоваться функцией распределения.
. Для математического описания такого закона распределения удобно пользоваться функцией распределения.
Предположим, что игрок I выбирает число  из интервала
из интервала ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) согласно функции распределения
согласно функции распределения 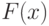 . Тогда для любой чистой стратегии
. Тогда для любой чистой стратегии  игрока II математическое ожидание выигрыша
игрока II математическое ожидание выигрыша 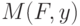 , если оно существует, будет равно
, если оно существует, будет равно
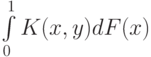 .
.
Пусть игрок II выбирает число  из интервала
из интервала ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) согласно функции распределения
согласно функции распределения 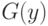 . Тогда математическое ожидание выигрыша
. Тогда математическое ожидание выигрыша 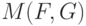 , если оно существует, будет равно
, если оно существует, будет равно
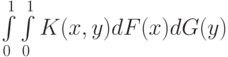 .
.
Предположим, что существует
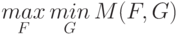 и
и 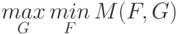
Выражение 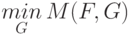 означает, что определяется такой вид функции распределения
означает, что определяется такой вид функции распределения 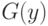 , который минимизирует выражение
, который минимизирует выражение 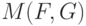 при заданной функции распределения
при заданной функции распределения 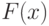 . Тогда выполняется следующее неравенство:
. Тогда выполняется следующее неравенство:
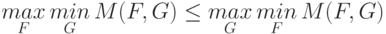 |
( 10.3) |
В теории игр доказывается, что, если функция выигрыша непрерывна по  и
и  , то
, то
 |
( 10.4) |
Общее значение обеих частей этого равенства называется значением игры и обозначается 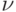 .
.
Если существуют такие  и
и  , что выполняются неравенства (10.2.), то значение игры равно
, что выполняются неравенства (10.2.), то значение игры равно 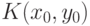 .
.
Если выполняется (10.4.), то у игрока I имеется такая стратегия (функция распределения) 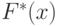 , что математическое ожидание выигрыша будет
, что математическое ожидание выигрыша будет
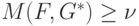
для любой стратегии игрока II 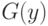 .
.
Аналогично, если выполняется (10.4.) , то существует функция распределения 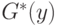 игрока II, при использовании которой математическое ожидание выигрыша будет
игрока II, при использовании которой математическое ожидание выигрыша будет
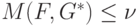
для любой стратегии игрока I 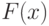 .
.
Стратегии 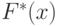 и
и 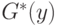 называются оптимальными стратегиями игроков I и II, соответственно. Пара
называются оптимальными стратегиями игроков I и II, соответственно. Пара 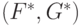 называется решением игры в смешанных стратегиях, а значение игры равно
называется решением игры в смешанных стратегиях, а значение игры равно
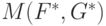 .
.