|
мне задали дистанционное задание на сертификат,но я не могу его найти |
Основные понятия теории вероятностей
Введение
Теория вероятностей изучает объективные закономерности, присущие массовым случайным явлениям. Значительная часть содержащихся в лекциях сведений дается в рамках вполне конкретных задач и примеров. Методам данной теории отведено три лекции.
Опыт с равновероятными исходами
Рассмотрим такой простой опыт, как бросание монеты. Он имеет два взаимно исключающих исхода: выпадение "орла" и выпадение "решки". Рассмотрим некоторый опыт с конечным числом взаимно исключающих друг друга исходов, которые равноправны по отношению к условию данного опыта, то есть равновероятны. Обозначим как  некоторое событие, связанное с указанными исходами.
некоторое событие, связанное с указанными исходами.
Вероятность
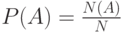 |
( 2.1) |
где  — общее число исходов рассматриваемого опыта,
— общее число исходов рассматриваемого опыта, 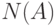 — число тех из них, которые приводят к наступлению события
— число тех из них, которые приводят к наступлению события  . Например, при бросании монеты имеется 2 взаимно исключающих равновероятных исхода (выпадение "орла" и выпадение "решки"), и если
. Например, при бросании монеты имеется 2 взаимно исключающих равновероятных исхода (выпадение "орла" и выпадение "решки"), и если  — любое из этих событий, то вероятность
— любое из этих событий, то вероятность 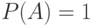 , поскольку
, поскольку 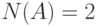 .
.
Накопленные практикой многочисленные наблюдения выявили одну замечательную закономерность, которая позволяет придать глубокий смысл понятию вероятности как в рассмотренном выше опыте с равновероятными исходами, так и в самом общем случае. А именно: предположим, что рассматриваемый опыт, явление и тому подобное могут быть воспроизведены многократно. Так что, в принципе, осуществима целая серия одинаковых и независимых друг от друга испытаний, в каждом из которых по воле случая происходит или не происходит интересующее наблюдателя событие  . Пусть
. Пусть  обозначает число всех опытов в отдельной серии испытаний и n
обозначает число всех опытов в отдельной серии испытаний и n  — число тех из них, в которых осуществляется событие
— число тех из них, в которых осуществляется событие  . Отношение
. Отношение 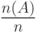 называется частотой события
называется частотой события  в данной серии испытаний. Оказывается, в различных сериях испытаний соответствующие частоты
в данной серии испытаний. Оказывается, в различных сериях испытаний соответствующие частоты 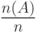 при больших
при больших  практически совпадают. И P
практически совпадают. И P  приблизительно равно
приблизительно равно 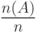 .
.
Формально это нужно понимать следующим образом:
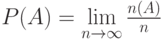 |
( 2.2) |
Согласно этой эмпирически установленной закономерности вероятность 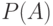 события
события  характеризует долю тех случаев в большой серии опытов, которые приводят к наступлению события.
характеризует долю тех случаев в большой серии опытов, которые приводят к наступлению события.
При подсчете вероятностей большую пользу оказывают комбинаторные формулы. Приведем наиболее важные из них.
Закон сложения вероятностей
Предположим, что в результате рассматриваемого опыта или явления происходит один из взаимно исключающих друг друга исходов, которые будем обозначать греческой буквой  и называть элементарными событиями или элементарными исходами.
и называть элементарными событиями или элементарными исходами.
Будем говорить, что событие  связано с рассматриваемым опытом (или с элементарными исходами
связано с рассматриваемым опытом (или с элементарными исходами  ), если по каждому элементарному исходу
), если по каждому элементарному исходу  можно точно судить о том, осуществляется или нет данное событие
можно точно судить о том, осуществляется или нет данное событие  . Обозначим тем же символом
. Обозначим тем же символом  совокупность (иначе множество) всех элементарных исходов
совокупность (иначе множество) всех элементарных исходов  , в результате которых наступает событие
, в результате которых наступает событие  . Очевидно, событие
. Очевидно, событие  происходит тогда и только тогда, когда наступает один из элементарных исходов
происходит тогда и только тогда, когда наступает один из элементарных исходов  , входящих в указанную совокупность
, входящих в указанную совокупность  . Вместо того чтобы говорить об исходном событии
. Вместо того чтобы говорить об исходном событии  , можно говорить лишь о событии "наступает элементарный исход
, можно говорить лишь о событии "наступает элементарный исход  , входящий в совокупность
, входящий в совокупность  ".
".
События 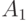 и
и 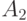 называют равными (
называют равными (  ), если осуществление события
), если осуществление события 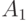 влечет за собой осуществление события
влечет за собой осуществление события 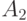 и наоборот, осуществление
и наоборот, осуществление 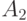 влечет за собой осуществление события
влечет за собой осуществление события 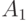 .
.
События 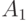 и
и 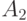 называются несовместными или непересекающимися, если наступление одного из этих событий исключает возможность наступления другого, иначе говоря,
называются несовместными или непересекающимися, если наступление одного из этих событий исключает возможность наступления другого, иначе говоря, 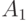 и
и 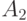 не могут произойти одновременно.
не могут произойти одновременно.
Объединением или суммой событий 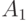 и
и 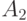 называется событие
называется событие  , которое означает осуществление хотя бы одного из событий
, которое означает осуществление хотя бы одного из событий 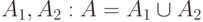 где
где  — специальный символ объединения. Аналогично определяется объединение событий
— специальный символ объединения. Аналогично определяется объединение событий 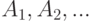 , обозначаемое как
, обозначаемое как 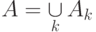 .
.
Пересечением или произведением событий 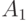 и
и 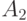 называется событие
называется событие  , которое означает осуществление и события
, которое означает осуществление и события 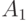 , и события
, и события 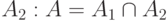 , где
, где  — специальный символ пересечения. Аналогично определяется произведение событий
— специальный символ пересечения. Аналогично определяется произведение событий 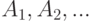 , обозначаемое как
, обозначаемое как 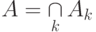 .
.
Разностью событий 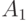 и
и 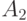 называется событие
называется событие  , которое означает, что происходит событие
, которое означает, что происходит событие 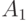 , но не происходит событие
, но не происходит событие 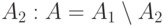 . Дополнительным к событию
. Дополнительным к событию  называется событие
называется событие 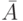 , которое означает, что событие
, которое означает, что событие  не происходит:
не происходит: 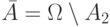 .
.
Рассмотрим несовместные события 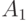 и
и 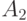 . Представим себе, что проводится серия одинаковых и независимых между собой опытов, результатом каждого из которых могут быть указанные события
. Представим себе, что проводится серия одинаковых и независимых между собой опытов, результатом каждого из которых могут быть указанные события 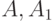 и
и 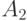 . Пусть
. Пусть  — число всех испытаний,
— число всех испытаний, 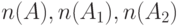 — число тех из них, которые привели к наступлению соответствующих событий
— число тех из них, которые привели к наступлению соответствующих событий 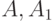 и
и 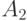 . Если в каком-то опыте произошло событие
. Если в каком-то опыте произошло событие  , то это значит,
, то это значит, 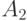 (одновременно
(одновременно 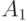 и
и 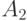 произойти не могут, так как по условию они являются несовместимыми). Поэтому числа
произойти не могут, так как по условию они являются несовместимыми). Поэтому числа 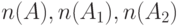 связаны между собой следующим равенством:
связаны между собой следующим равенством:
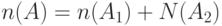 .
.
Следовательно, частоты рассматриваемых событий таковы, что
 .
.
При достаточно большом числе испытаний частоты практически совпадают с соответствующими вероятностями, так что вероятности рассматриваемых событий  ,
, 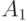 и
и 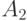 должны быть связаны между собой следующим равенством:
должны быть связаны между собой следующим равенством:
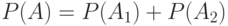 .
.
Полученное равенство является выражением так называемого закона сложения вероятностей , согласно которому для любых непересекающихся событий 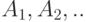 . вероятность их объединения
. вероятность их объединения  есть
есть
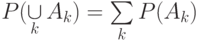 |
( 2.3) |

