|
мне задали дистанционное задание на сертификат,но я не могу его найти |
Основные понятия теории вероятностей
Условные вероятности
При анализе того или иного явления часто возникает вопрос о том, как влияет на возможность осуществления некоторого события  наступление другого события
наступление другого события  . Простейшим примером связи событий
. Простейшим примером связи событий  и
и  может служить следующее: наступление
может служить следующее: наступление  ведет к обязательному осуществлению события
ведет к обязательному осуществлению события  или, наоборот, наступление
или, наоборот, наступление  исключает возможность осуществления события
исключает возможность осуществления события  . В теории вероятностей характеристикой связи событий
. В теории вероятностей характеристикой связи событий  и
и  служит так называемая условная вероятность
служит так называемая условная вероятность 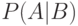 события
события  при условии
при условии  , определяемая как
, определяемая как
 |
( 2.4) |
(предполагается, что вероятность события  является положительной).
является положительной).
Величина 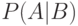 может рассматриваться как вероятность осуществления события
может рассматриваться как вероятность осуществления события  при условии наступления события
при условии наступления события  . Поясним это на примере опыта с конечным числом равновероятных элементарных исходов
. Поясним это на примере опыта с конечным числом равновероятных элементарных исходов  . Пусть
. Пусть  — число всех элементарных исходов,
— число всех элементарных исходов,  — число тех из них, которые приводят к наступлению события
— число тех из них, которые приводят к наступлению события  . В этом случае вероятности событий
. В этом случае вероятности событий  и
и 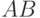 суть
суть 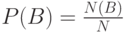 и
и 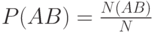 , так что условная вероятность
, так что условная вероятность 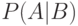 выражается следующей формулой:
выражается следующей формулой:
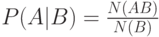 |
( 2.5) |
Здесь  — число всех элементарных исходов
— число всех элементарных исходов  , возможных при условии наступления события
, возможных при условии наступления события  , а
, а 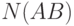 — число тех из них, которые приводят к осуществлению события
— число тех из них, которые приводят к осуществлению события  . В соответствии с общей формулой 2.1. равенство 2.5. определяет вероятность события
. В соответствии с общей формулой 2.1. равенство 2.5. определяет вероятность события  в новых условиях, которые возникают при наступлении события
в новых условиях, которые возникают при наступлении события  .
.
Условные вероятности обладают всеми свойствами, присущими обычным вероятностям. Именно,
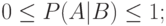
если наступление события  исключает возможность осуществления
исключает возможность осуществления 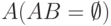 , то
, то
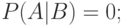
если событие  ведет к обязательному осуществлению события
ведет к обязательному осуществлению события 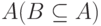 , то
, то
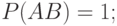
если событие  есть объединение непересекающихся событий
есть объединение непересекающихся событий 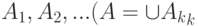 , то
, то
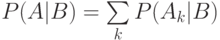 .
.
Действительно, если 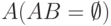 , то есть
, то есть  и
и  являются непересекающимися, то
являются непересекающимися, то 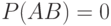 , откуда и
, откуда и 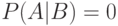 ; если
; если 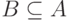 , то
, то 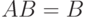 и
и 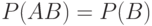 , что равносильно равенству
, что равносильно равенству 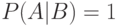 ; если событие
; если событие  есть объединение непересекающихся событий
есть объединение непересекающихся событий 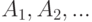 , то произведение
, то произведение 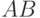 является объединением непересекающихся событий
является объединением непересекающихся событий 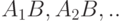 . и согласно формуле 2.3.
. и согласно формуле 2.3.
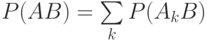
откуда и вытекает указанный выше закон сложения условных вероятностей.
При нахождении вероятности того или иного события  бывает удобным сначала считать осуществившимся подходящим образом выбранное событие
бывает удобным сначала считать осуществившимся подходящим образом выбранное событие  и определить условную вероятность
и определить условную вероятность 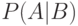 как вероятность события
как вероятность события  в новых условиях, когда событие
в новых условиях, когда событие  является достоверным. Если имеется некоторая полная система несовместных событий
является достоверным. Если имеется некоторая полная система несовместных событий 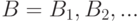 , то есть таких, что хотя бы одно из них обязательно осуществится, то вероятность
, то есть таких, что хотя бы одно из них обязательно осуществится, то вероятность 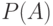 события
события  выражается через соответствующие условные вероятности
выражается через соответствующие условные вероятности 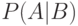 при помощи следующей формулы:
при помощи следующей формулы:
 |
( 2.6) |
Это соотношение называется формулой полной вероятности. Оно вытекает из закона сложения вероятностей. Действительно, объединение событий 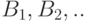 . по условию является достоверным событием
. по условию является достоверным событием  ; следовательно,
; следовательно, 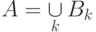 и
и
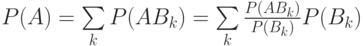 .
.
Общая теоретико-вероятностная схема
Числовая величина  , значения которой зависят от элементарных исходов
, значения которой зависят от элементарных исходов 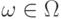 , называется случайной величиной:
, называется случайной величиной:
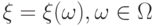 .
.
Говорят, что задано распределение вероятностей случайной величины  , если определены вероятности
, если определены вероятности 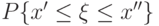 всевозможных событий
всевозможных событий 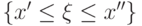 , каждое из которых означает, что
, каждое из которых означает, что  принимает одно из значений
принимает одно из значений 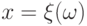 в соответствующих пределах
в соответствующих пределах 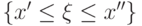 .
.
Случайная величина  имеет дискретное распределение (иначе, величина
имеет дискретное распределение (иначе, величина  является дискретной), если в зависимости от элементарных исходов
является дискретной), если в зависимости от элементарных исходов  величина
величина 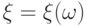 принимает конечное или счетное число различных значений
принимает конечное или счетное число различных значений  с соответствующими вероятностями
с соответствующими вероятностями 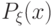 :
:
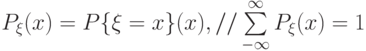 .
.
Для таких величин
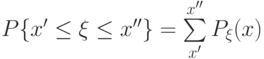 |
( 2.7) |
(суммирование идет по конечному или счетному числу значений  в пределах
в пределах 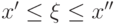 , которые может принять дискретная случайная величина
, которые может принять дискретная случайная величина  ).
).
Говорят, что 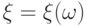 имеет непрерывное распределение вероятностей, если для любых
имеет непрерывное распределение вероятностей, если для любых 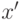 и
и 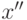
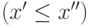
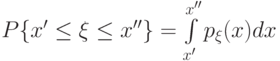 |
( 2.8) |
где 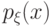 — некоторая неотрицательная интегрируемая функция,
— некоторая неотрицательная интегрируемая функция,
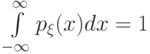 ,
,
называемая плотностью распределения вероятностей величины  .
.
Рассмотрим дискретную случайную величину  . Говорят, что
. Говорят, что  имеет математическое ожидание, если
имеет математическое ожидание, если
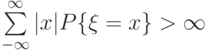 ;
;
математическим ожиданием (или средним значением ) называется выражение
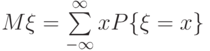 |
( 2.9) |
(суммирование идет по конечному или счетному числу значений 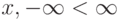 которые может принимать дискретная величина
которые может принимать дискретная величина  ).
).
Если задано распределение вероятностей случайной величины  , то математическое ожидание случайной величины вида
, то математическое ожидание случайной величины вида 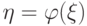 может быть подсчитано по следующей формуле:
может быть подсчитано по следующей формуле:
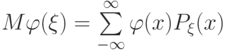 |
( 2.10) |
Как видно из самого определения, математическое ожидание обладает следующими свойствами:
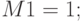
для любой постоянной 
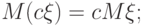
для любых величин 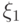 и
и 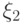 имеющих математические ожидания
имеющих математические ожидания  и
и  ,
,
 |
( 2.11) |
если 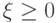 , то
, то 
если  , то
, то
 |
( 2.12) |
если случайные величины 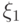 и
и 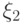 независимы, то
независимы, то
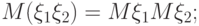 |
( 2.13) |
Математическое ожидание определяется и для непрерывно распределенных случайных величин. Именно, всякая случайная величина  может быть сколь угодно точно аппроксимирована дискретными величинами. Например, если разбить действительную прямую
может быть сколь угодно точно аппроксимирована дискретными величинами. Например, если разбить действительную прямую 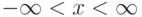 точками
точками 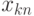 ,
, 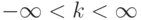 так, чтобы
так, чтобы
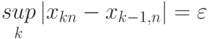 ,
,
и определить дискретные случайные величины 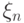 как
как
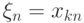 при
при 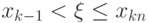 ,
,
то, очевидно, 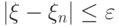 , где
, где 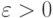 можно выбрать сколь угодно малыми. Если взять последовательность величин
можно выбрать сколь угодно малыми. Если взять последовательность величин 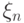 такого типа
такого типа 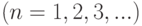 , для которых
, для которых
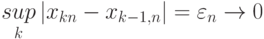 ,
,
то
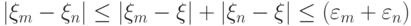
и, согласно неравенству (2.12.) ,
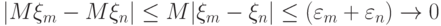
при 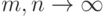 . Следовательно, существует предел
. Следовательно, существует предел
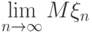 .
.
Для непрерывно распределенной случайной величины  такой предел и называется математическим ожиданием (или средним значением):
такой предел и называется математическим ожиданием (или средним значением):
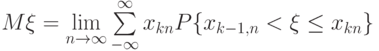 .
.


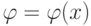 — некоторая
— некоторая