|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Потоки
Метод увеличивающих путей
При внимательном рассмотрении рисунка 16.1 можно обнаружить, что
представленный на нем поток не является максимальным, так как существует
ориентированный путь 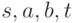 , на каждом ребре которого поток
можно
увеличить на 1. Иногда поток можно увеличить и при отсутствии таких
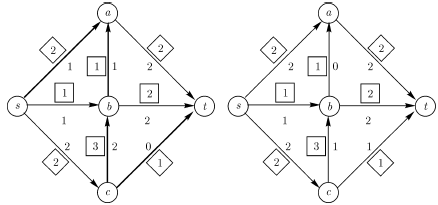
"недогруженных" путей из источника в сток. Рассмотрим пример сети
и потока
на рис. 16.2 слева. Среди ребер,
выходящих
из источника, только на ребре
, на каждом ребре которого поток
можно
увеличить на 1. Иногда поток можно увеличить и при отсутствии таких
"недогруженных" путей из источника в сток. Рассмотрим пример сети
и потока
на рис. 16.2 слева. Среди ребер,
выходящих
из источника, только на ребре 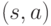 можно было бы увеличить
поток на 1. Но тогда нарушится условие сохранения потока в вершине
можно было бы увеличить
поток на 1. Но тогда нарушится условие сохранения потока в вершине  , а дальше эту дополнительную единицу
потока передать нельзя, так как ребро
, а дальше эту дополнительную единицу
потока передать нельзя, так как ребро 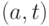 полностью загружено.
Можно, однако, заметить, что в вершину
полностью загружено.
Можно, однако, заметить, что в вершину  входит еще
ребро
входит еще
ребро 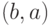 с положительным потоком на нем. Если одновременно увеличить поток на
ребре
с положительным потоком на нем. Если одновременно увеличить поток на
ребре 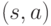 и уменьшить на ребре
и уменьшить на ребре 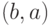 на 1, то
условие сохранения
в вершине
на 1, то
условие сохранения
в вершине  останется выполненным. Но теперь будет нарушено
условие
сохранения в вершине
останется выполненным. Но теперь будет нарушено
условие
сохранения в вершине  . Это легко исправить, уменьшив на 1 поток
на ребре
. Это легко исправить, уменьшив на 1 поток
на ребре 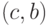 . В результате возникает нарушение в вершине
. В результате возникает нарушение в вершине  , но
и оно будет устранено, если мы увеличим на 1 поток на
ребре
, но
и оно будет устранено, если мы увеличим на 1 поток на
ребре 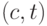 . После
этого условие сохранения будет выполнено во всех внутренних вершинах,
а величина потока увеличится на 1. Новый поток показан на рисунке 16.2.
. После
этого условие сохранения будет выполнено во всех внутренних вершинах,
а величина потока увеличится на 1. Новый поток показан на рисунке 16.2.
В этом примере, как и в предыдущем, удалось найти
путь 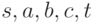 (выделен на рисунке), вдоль которого можно направить дополнительный поток.
Отличие в том, что этот путь не ориентированный - при движении вдоль него
от источника к стоку некоторые ребра проходятся в направлении ориентации
(прямые), другие против ориентации (обратные). При этом все прямые ребра
пути недогружены, то есть поток на каждом из них не достигает пропускной
способности, а на каждом из обратных ребер имеется положительный поток.
Благодаря этому можно увеличить поток на всех прямых ребрах пути
и уменьшить на всех обратных на одну и ту же величину. В результате условие
сохранения потока во внутренних вершинах по-прежнему выполняется,
а величина потока увеличивается.
(выделен на рисунке), вдоль которого можно направить дополнительный поток.
Отличие в том, что этот путь не ориентированный - при движении вдоль него
от источника к стоку некоторые ребра проходятся в направлении ориентации
(прямые), другие против ориентации (обратные). При этом все прямые ребра
пути недогружены, то есть поток на каждом из них не достигает пропускной
способности, а на каждом из обратных ребер имеется положительный поток.
Благодаря этому можно увеличить поток на всех прямых ребрах пути
и уменьшить на всех обратных на одну и ту же величину. В результате условие
сохранения потока во внутренних вершинах по-прежнему выполняется,
а величина потока увеличивается.
Приведенный пример иллюстрирует общий метод, на котором основаны многие алгоритмы решения задачи о максимальном потоке - метод увеличивающих путей. Он является обобщением метода увеличивающих путей для задачи о паросочетании. Введем необходимые понятия и докажем теорему, обосновывающую этот метод.
Допустим, имеется сеть  и в ней поток
и в ней поток  . Пусть
. Пусть 
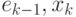 -
неориентированный
путь в сети. Ребро
-
неориентированный
путь в сети. Ребро 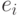 назовем прямым ребром этого пути, если
назовем прямым ребром этого пути, если 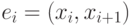 , и обратным, если
, и обратным, если 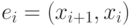 .
Путь назовем подходящим
относительно потока
.
Путь назовем подходящим
относительно потока  ,
если для каждого прямого ребра f(ei)< c(ei), а для каждого
обратного
,
если для каждого прямого ребра f(ei)< c(ei), а для каждого
обратного 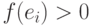 . Таким образом, на каждом прямом ребре
подходящего пути поток можно увеличить, а на каждом обратном - уменьшить. Увеличивающий путь - это подходящий путь из источника
в сток.
. Таким образом, на каждом прямом ребре
подходящего пути поток можно увеличить, а на каждом обратном - уменьшить. Увеличивающий путь - это подходящий путь из источника
в сток.
Лемма 3. Если относительно потока  имеется
увеличивающий путь, то этот поток не максимален.
имеется
увеличивающий путь, то этот поток не максимален.
Доказательство. Пусть  - увеличивающий путь для потока
- увеличивающий путь для потока  ,
,  - множество всех
прямых,
- множество всех
прямых,  - множество всех обратных ребер этого пути.
Положим,
- множество всех обратных ребер этого пути.
Положим,
 .
.Тогда на каждом прямом ребре пути можно увеличить поток на величину 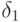 , а на каждом обратном - уменьшить на величину
, а на каждом обратном - уменьшить на величину 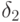 . Возьмем
. Возьмем 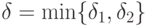
и определим на ребрах сети новую функцию 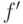 :
:
 .
.Легко видеть, что условия (1) и (2) для функции 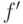 выполняются,
так
что эта функция является потоком. Вместе с тем, очевидно,
выполняются,
так
что эта функция является потоком. Вместе с тем, очевидно,  , причем
, причем 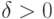 .
.