|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Потоки
Теорема 1. Поток максимален тогда и только тогда, когда относительно него нет увеличивающего пути. Максимальная величина потока равна минимальной пропускной способности разреза данной сети.
Доказательство. Если поток максимален, то из леммы 3 следует, что
увеличивающего пути нет. Обратно, пусть  - поток,
относительно
которого нет увеличивающего пути. Покажем, что этот поток максимален.
Для этого рассмотрим множество
- поток,
относительно
которого нет увеличивающего пути. Покажем, что этот поток максимален.
Для этого рассмотрим множество  , состоящее из всех вершин сети,
достижимых подходящими путями из вершины
, состоящее из всех вершин сети,
достижимых подходящими путями из вершины  ,
,  .
Так как увеличивающих путей нет, то
.
Так как увеличивающих путей нет, то 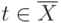 ,
так что
,
так что  - разрез.
Пусть
- разрез.
Пусть 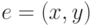 - ребро этого разреза. Вершина
- ребро этого разреза. Вершина  достижима из
достижима из  подходящим путем, а вершина
подходящим путем, а вершина  недостижима.
Тогда
недостижима.
Тогда 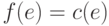 , так как иначе к подходящему пути,
ведущему из
, так как иначе к подходящему пути,
ведущему из  в
в  , можно было бы добавить ребро
, можно было бы добавить ребро  и вершину
и вершину  ,
и получился бы подходящий путь из
,
и получился бы подходящий путь из  в
в  . Итак, на
каждом
ребре разреза
. Итак, на
каждом
ребре разреза  поток равен пропускной способности,
следовательно,
поток равен пропускной способности,
следовательно, 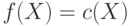 . Аналогично, рассматривая ребра из
множества
. Аналогично, рассматривая ребра из
множества  , убеждаемся, что поток на каждом таком ребре равен 0,
в противном случае опять можно было бы продолжить некоторый подходящий путь
до вершины из
, убеждаемся, что поток на каждом таком ребре равен 0,
в противном случае опять можно было бы продолжить некоторый подходящий путь
до вершины из  . Следовательно,
. Следовательно,  .
Применяя лемму 1,
получаем
.
Применяя лемму 1,
получаем
 .
.По лемме 2, величина любого потока не превосходит пропускной способности
любого разреза. Значит,  - максимальный поток,
а
- максимальный поток,
а  - разрез с минимальной пропускной
способностью.
- разрез с минимальной пропускной
способностью.
Многие известные алгоритмы построения максимального потока основаны на
этой теореме и различаются, в частности, стратегией поиска увеличивающих
путей. Первый алгоритм, для которого была получена верхняя оценка
трудоемкости, предложили Эдмондс и Карп в 1972 г. В этом алгоритме всегда
ищется кратчайший (по числу ребер) увеличивающий путь. Удобно этот поиск
вести не на исходной сети  , а на остаточной сети
, а на остаточной сети  ,
которая при заданном на сети
,
которая при заданном на сети  потоке
потоке  определяется
следующим
образом. Множество вершин, источник и сток у остаточной сети те же, что
у исходной. Пусть
определяется
следующим
образом. Множество вершин, источник и сток у остаточной сети те же, что
у исходной. Пусть  - ребро исходной сети. Тогда
- ребро исходной сети. Тогда
- если f(e)< c(e), то ребро
 включается в сеть
включается в сеть  и ему
в этой сети присваивается пропускная
способность
и ему
в этой сети присваивается пропускная
способность 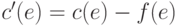 ;
; - если
 , то к сети
, то к сети  добавляется ребро
противоположного
направления
добавляется ребро
противоположного
направления 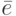 с пропускной способностью
с пропускной способностью  .
.
Легко видеть, что увеличивающие пути в исходной сети находятся во взаимно
однозначном соответствии с ориентированными путями из источника в сток в
остаточной сети. В алгоритме Эдмондса--Карпа нужно в остаточной сети искать
кратчайший ориентированный путь из  в
в  . Это можно
сделать за
линейное время с помощью поиска в ширину. Если увеличивающий путь
обнаружен, поток увеличивается, как описано в доказательстве леммы 3, для
нового потока строится остаточная сеть и т.д., пока не будет построен
поток, относительно которого нет увеличивающего пути (в остаточной сети
нет ориентированного пути из источника в сток. Общая оценка трудоемкости
алгоритма Эдмондса--Карпа
. Это можно
сделать за
линейное время с помощью поиска в ширину. Если увеличивающий путь
обнаружен, поток увеличивается, как описано в доказательстве леммы 3, для
нового потока строится остаточная сеть и т.д., пока не будет построен
поток, относительно которого нет увеличивающего пути (в остаточной сети
нет ориентированного пути из источника в сток. Общая оценка трудоемкости
алгоритма Эдмондса--Карпа 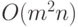 . В настоящее время известны
и более быстрые алгоритмы для задачи о максимальном потоке.
. В настоящее время известны
и более быстрые алгоритмы для задачи о максимальном потоке.
