|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Лекция 9: Независимые множества, клики, вершинные покрытия.
Стратегия перебора для задачи о независимом множестве
Пусть  - граф, в котором требуется найти наибольшее
независимое
множество. Выберем в нем произвольную вершину
- граф, в котором требуется найти наибольшее
независимое
множество. Выберем в нем произвольную вершину  . Обозначим
через
. Обозначим
через 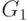 подграф, получающийся удалением из
графа
подграф, получающийся удалением из
графа  вершины
вершины  , т.е.
, т.е. 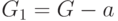 , а
через
, а
через 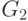 - подграф,
получающийся удалением из
- подграф,
получающийся удалением из  всех вершин, смежных
с
всех вершин, смежных
с  . На рисунке 9.2 показаны графы
. На рисунке 9.2 показаны графы 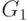 и
и 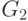 , получающиеся из
графа
, получающиеся из
графа  , изображенного на рис. 9.1, при
, изображенного на рис. 9.1, при 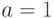 .
.
Пусть  - какое-нибудь независимое множество
графа
- какое-нибудь независимое множество
графа  . Если
оно не содержит вершины
. Если
оно не содержит вершины  , то оно является независимым множеством
графа
, то оно является независимым множеством
графа 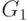 . Если же
. Если же 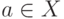 , то никакая вершина,
смежная
с
, то никакая вершина,
смежная
с  , не принадлежит
, не принадлежит  . В этом случае
множество
. В этом случае
множество  является независимым множеством
графа
является независимым множеством
графа 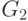 . Заметим, что в графе
. Заметим, что в графе 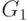 на одну
вершину меньше, чем в исходном графе
на одну
вершину меньше, чем в исходном графе  . Если
вершина
. Если
вершина  не является изолированной, то
и в графе
не является изолированной, то
и в графе 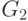 вершин меньше, чем в графе
вершин меньше, чем в графе  . Таким
образом, задача о независимом
множестве для графа
. Таким
образом, задача о независимом
множестве для графа  свелась к решению той же задачи для двух
графов меньшего размера. Это приводит к рекуррентному соотношению для
числа независимости:
свелась к решению той же задачи для двух
графов меньшего размера. Это приводит к рекуррентному соотношению для
числа независимости:
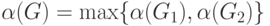
и к рекурсивному алгоритму для нахождения наибольшего независимого
множества графа 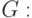 найдем наибольшее независимое
множество
найдем наибольшее независимое
множество 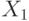 графа
графа 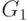 , затем наибольшее
независимое множество
, затем наибольшее
независимое множество 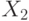 графа
графа 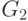 и выберем
большее из этих двух множеств. В целом процесс
решения задачи при этом можно рассматривать как исчерпывающий поиск
в возникающем дереве подзадач. Чтобы не путать вершины дерева и вершины
графа, вершины дерева будем называть узлами. Узел, не являющийся листом,
называется внутренним узлом. Каждому внутреннему узлу дерева соответствует
некоторый граф
и выберем
большее из этих двух множеств. В целом процесс
решения задачи при этом можно рассматривать как исчерпывающий поиск
в возникающем дереве подзадач. Чтобы не путать вершины дерева и вершины
графа, вершины дерева будем называть узлами. Узел, не являющийся листом,
называется внутренним узлом. Каждому внутреннему узлу дерева соответствует
некоторый граф  и некоторая вершина этого графа
и некоторая вершина этого графа  .
Вершину
.
Вершину  можно выбирать произвольно, но она не должна быть
изолированной вершиной графа
можно выбирать произвольно, но она не должна быть
изолированной вершиной графа  . Внутренний узел имеет двух
сыновей -
левого и правого. Левому сыну соответствует подграф графа
. Внутренний узел имеет двух
сыновей -
левого и правого. Левому сыну соответствует подграф графа  ,
получаемый удалением вершины
,
получаемый удалением вершины  , а правому - подграф,
получаемый
удалением всех вершин, смежных с
, а правому - подграф,
получаемый
удалением всех вершин, смежных с  . Корню дерева соответствует
исходный граф. Листьям соответствуют подграфы, не имеющие ребер, то есть
подграфы, у которых все вершины изолированные. Множества вершин этих
подграфов - это независимые множества исходного графа.
. Корню дерева соответствует
исходный граф. Листьям соответствуют подграфы, не имеющие ребер, то есть
подграфы, у которых все вершины изолированные. Множества вершин этих
подграфов - это независимые множества исходного графа.
Для нахождения наибольшего независимого множества не обязательно строить все дерево полностью, а достаточно обойти его в том или ином порядке, запоминая на каждом шаге только небольшую часть информации об устройстве этого дерева. Можно, например, применить поиск в глубину для обхода дерева: сначала пройти от корня до некоторого листа, затем вернуться к предку этого листа и искать следующий лист, и т.д.
Для одного и того же графа могут получиться разные деревья в зависимости
от того, как выбирается активная вершина  в каждом узле
дерева. Может быть различным и число листьев в этих деревьях, а значит,
и трудоемкость алгоритма, основанного на обходе дерева. Однако в любом
случае листьев в дереве будет не меньше, чем максимальных независимых
множеств у графа, так как каждое из этих множеств будет соответствовать
некоторому листу. Так, для графа
в каждом узле
дерева. Может быть различным и число листьев в этих деревьях, а значит,
и трудоемкость алгоритма, основанного на обходе дерева. Однако в любом
случае листьев в дереве будет не меньше, чем максимальных независимых
множеств у графа, так как каждое из этих множеств будет соответствовать
некоторому листу. Так, для графа  , т.е. графа, состоящего
из
, т.е. графа, состоящего
из  компонент связности, каждая из которых изоморфна
графу
компонент связности, каждая из которых изоморфна
графу 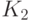 ,
в дереве подзадач будет
,
в дереве подзадач будет 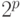 листьев.
листьев.