Лекция 9: Независимые множества, клики, вершинные покрытия.

Будем теперь рассматривать множества из одно за другим и пусть - очередное такое множество. Положим 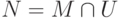. Если не является максимальным независимым множеством графа 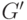, то переходим к следующему элементу списка . Если же - максимальное независимое множество в 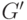, то рассматриваем множество . Если оно является лексикографически первым среди максимальных независимых множеств подграфа, порожденного множеством 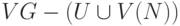, то включаем в список .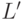

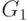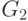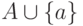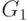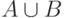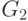Выберем в графе произвольную вершину и пусть - множество всех вершин графа, смежных с (окрестность вершины ), - множество всех вершин, не смежных с и отличных от . Обозначим через подграф, получающийся удалением из графа вершины , а через подграф, получающийся удалением из всех вершин множества . Иначе говоря, - подграф графа , порожденный множеством , а - подграф, порожденный множеством .

Допустим, что имеется список 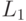всех максимальных независимых множеств графа 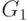. На основании вышеизложенного можно предложить следующую процедуру получения списка всех максимальных независимых множеств графа .

1. Взять очередной элемент списка .
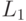2. Если 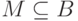, то добавить к списку множество 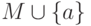и перейти к 1, иначе добавить к списку множество .
3. Если множество не является максимальным независимым множеством в графе 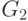, то перейти к 1.
4. Если множество 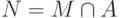является лексикографически первым максимальным независимым множеством подграфа, порожденного множеством 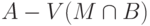, то добавить к списку множество .
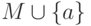5. Если список 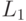не исчерпан, перейти к 1.

Начиная с одновершинного графа (у которого список максимальных независимых множеств состоит из одного элемента), добавляя последовательно по одной вершине, получаем последовательность графов 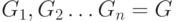. Применяя для каждого описанный алгоритм для построения списка всех максимальных независимых множеств графа 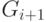по такому списку для графа 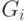, в конце концов получим список всех максимальных независимых множеств графа . По сути дела, этот алгоритм представляет собой поиск в ширину в дереве вариантов. Для того чтобы не хранить все получающиеся списки, его можно преобразовать в поиск в глубину. 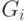Заметим, что приведенная процедура для каждого максимального независимого множества графа находит одно или два максимальных независимых множества графа 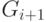. Одно из этих новых множеств рассматривается на следующем шаге, другое, если оно есть, запоминается в стеке.

Изложенный алгоритм можно применить для поиска наибольших независимых множеств в графах, про которые известно, что в них мало максимальных независимых множеств. Одним из классов графов с таким свойством является класс всех графов, не содержащих в качестве порожденного подграфа. Известно, что в графе с ребрами из этого класса число максимальных независимых множеств не превосходит 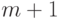.