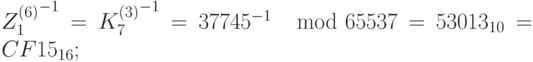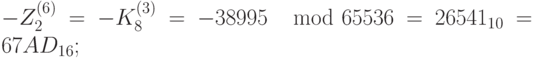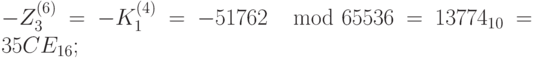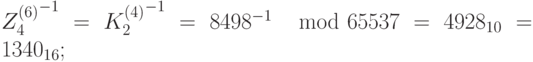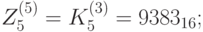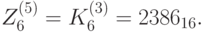|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Современные симметричные алгоритмы шифрования
7.7 Алгоритм IDEA
См. ([6])
В настоящее время используется большое количество самых разных алгоритмов блочного шифрования. Из всего многообразия мы расскажем лишь о тех алгоритмах, которые либо являются очень надежными, либо своим появлением оказали влияние на развитие криптографии. Одним из таких алгоритмов является IDEA.
Первый вариант шифра IDEA, предложенный Ксуеджа Лай (Xuejia Lai) и Джеймсом Масси (James Massey), появился в 1990 году. Он назывался PES (Proposed Encryption Standard, предложенный стандарт шифрования). В следующем году, после демонстрации Бихамом и Шамиром возможностей дифференциального криптоанализа, авторы усилили свой шифр против такого вскрытия и назвали новый алгоритм IPES (Improved Proposed Encryption Standard, улучшенный предложенный стандарт шифрования). В 1992 году название IPES было изменено на IDEA (International Data Encryption Algorithm, международный алгоритм шифрования данных).
IDEA основывается на некоторых впечатляющих теоретических положениях и, хотя криптоанализ добился некоторых успехов в отношении вариантов с уменьшенным количеством этапов, алгоритм все еще кажется сильным.
Его сегодняшняя известность объясняется тем, что он является частью PGP.
7.7.1 Обзор IDEA
IDEA является блочным шифром, он работает с 64-битовыми блоками открытого текста. Длина ключа - 128 битов. Для шифрования и дешифрирования используется один и тот же алгоритм.
Как и другие, уже рассмотренные блочные шифры IDEA использует и запутывание, и рассеяние. Философия, лежащая в основе проекта, представляет собой "объединение операций из различных алгебраических групп". Смешиваются три алгебраические операции, и все они могут быть легко реализованы как аппаратно, так и программно.
- Поразрядное сложение по модулю 2 (операция "исключающее ИЛИ"); операция обозначается через
 .
. - Сложение беззнаковых целых по модулю
 ; операция обозначается через
; операция обозначается через  .
. - Умножение целых по модулю
 , рассматриваемых как беззнаковые целые, за исключением того, что блок из 16 нулей рассматривается как
, рассматриваемых как беззнаковые целые, за исключением того, что блок из 16 нулей рассматривается как 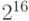 ; операция обозначается через
; операция обозначается через  .
.
Все операции выполняются над 16-битовыми субблоками. Эти три операции несогласованы в том смысле, что:
- никакая пара из этих трех операций не удовлетворяет ассоциативному закону, например,

- никакая пара из этих трех операций не удовлетворяет дистрибутивному закону, например,

Комбинирование этих трех операций обеспечивает комплексное преобразование входа, существенно затрудняя криптоанализ IDEA по сравнению с DES, который базируется исключительно на операции "исключающее ИЛИ".
Все эти операции (а в алгоритме используются только они, перестановки на битовом уровне не применяются) работают с 16-битовыми подблоками. (Этот алгоритм даже эффективнее на 16-битовых процессорах.)
7.7.2 Описание IDEA
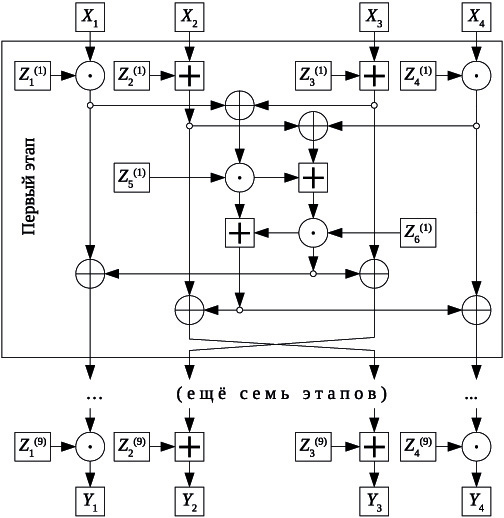
Схема IDEA представлена на рисунке 7.6. 64-битовый блок данных делится на четыре 16-битовых подблока: 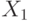 ,
, 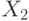 ,
, 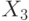 ,
,  . Эти четыре подблока становятся входными данными для первого этапа алгоритма. Всего в алгоритме восемь этапов. На каждом этапе четыре подблока подвергаются операциям XOR, сложениям и умножениям друг с другом и с шестью 16-битовыми подключами. Между этапами обмениваются местами второй и третий подблоки. Наконец, четыре подблока объединяются с четырьмя подключами в окончательном преобразовании.
. Эти четыре подблока становятся входными данными для первого этапа алгоритма. Всего в алгоритме восемь этапов. На каждом этапе четыре подблока подвергаются операциям XOR, сложениям и умножениям друг с другом и с шестью 16-битовыми подключами. Между этапами обмениваются местами второй и третий подблоки. Наконец, четыре подблока объединяются с четырьмя подключами в окончательном преобразовании.
На каждом этапе события происходят в следующей последовательности:
- Перемножаются
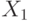 и первый подключ.
и первый подключ. - Складываются
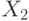 и второй подключ.
и второй подключ. - Складываются
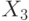 и третий подключ.
и третий подключ. - Перемножаются
 и четвертый подключ.
и четвертый подключ. - Выполняется XOR над результатами этапов (1) и (3).
- Выполняется XOR над результатами этапов (2) и (4).
- Перемножаются результаты этапа (5) и пятый подключ.
- Складываются результаты этапов (6) и (7).
- Перемножаются результаты этапа (8) и шестой подключ.
- Складываются результаты этапов (7) и (9).
- Выполняется XOR над результатами этапов (1) и (9).
- Выполняется XOR над результатами этапов (3) и (9).
- Выполняется XOR над результатами этапов (2) и (10).
- Выполняется XOR над результатами этапов (4) и (10).
Выходом этапа являются четыре подблока - результаты действий (11), (12), (13) и (14). Поменяйте местами два внутренних подблока (но не в последнем этапе), и вы получите исходные данные для следующего этапа.
Затем выполняется заключительный, 9-й этап преобразования:
- Перемножаются
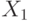 и первый подключ.
и первый подключ. - Складываются
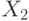 и второй подключ.
и второй подключ. - Складываются
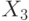 и третий подключ.
и третий подключ. - Перемножаются
 и четвертый подключ.
и четвертый подключ.
Наконец четыре подблока снова соединяются, образуя шифртекст.
Пример 7.11 Выполнить первый раунд зашифрования алгоритмом IDEA. Ключ: 1D52 34BC 891C 9C9B 1CC2 4363 A32B 132C, блок открытого текста: 89C1 B11D 63F0 FF23. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда  обозначают 16-битный блок
обозначают 16-битный блок 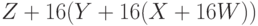 .
.
Решение.
Вначале выберем подключи первого раунда. Это первые 6 16-битных блоков ключа.
В обозначениях рисунка 7.6 имеем:  ,
, 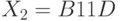 ,
, 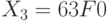 ,
, 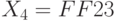 ,
, 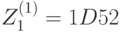 ,
, 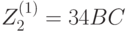 ,
, 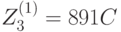 ,
,  ,
, 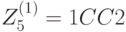 ,
,  .
.
Будем обозначать результат  -го шага в алгоритме параграфа 7.7.2 через
-го шага в алгоритме параграфа 7.7.2 через  .
.
Все операции будем проводить в шестнадцатеричной системе счисления. Результат применения одного раунда обозначим через 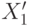 ,
, 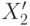 ,
, 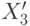 ,
,  .
.
Создание подключей 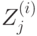 также относительно несложно. Алгоритм использует всего 52 подключа (по шесть для каждого из восьми циклов и еще четыре для заключительного этапа). Сначала 128-битовый ключ делят на восемь 16-битовых подключей. Это -- первые восемь подключей для алгоритма (шесть подключей -- для первого цикла и первые два подключа -- для второго цикла). Затем 128-битовый ключ циклически сдвигается влево на 25 бит и снова делится на восемь подключей. Первые четыре из них используют во втором цикле; последние четыре -- в третьем цикле. Ключ снова циклически сдвигается влево еще на 25 бит для получения следующих восьми подключей и т.д., пока выполнение алгоритма не завершится.
также относительно несложно. Алгоритм использует всего 52 подключа (по шесть для каждого из восьми циклов и еще четыре для заключительного этапа). Сначала 128-битовый ключ делят на восемь 16-битовых подключей. Это -- первые восемь подключей для алгоритма (шесть подключей -- для первого цикла и первые два подключа -- для второго цикла). Затем 128-битовый ключ циклически сдвигается влево на 25 бит и снова делится на восемь подключей. Первые четыре из них используют во втором цикле; последние четыре -- в третьем цикле. Ключ снова циклически сдвигается влево еще на 25 бит для получения следующих восьми подключей и т.д., пока выполнение алгоритма не завершится.
Расшифрование осуществляют аналогичным образом, за исключением того, что порядок использования подключей --- обратный, и ряд значений подключей заменяется на обратные значения. Порядок использования подключей при зашифровании и расшифровании приведён в таблице 7.10. Через 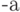 обозначается противоположный к
обозначается противоположный к  по модулю
по модулю 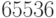 элемент, через
элемент, через 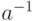 --- обратный по умножению по модулю
--- обратный по умножению по модулю 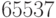 .
.
| Цикл | Подключи зашифрования | Подключи расшифрования |
|---|---|---|
| 1 | 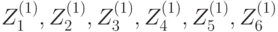 |
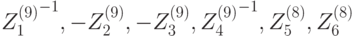 |
| 2 | 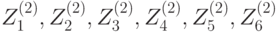 |
 |
| 3 |  |
 |
| 4 | 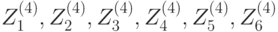 |
 |
| 5 |  |
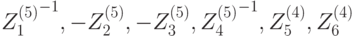 |
| 6 |  |
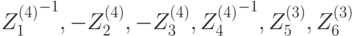 |
| 7 | 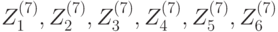 |
 |
| 8 |  |
 |
| 9 | 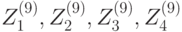 |
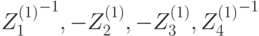 |
Пример 7.12 Имея ключ 1D52 34BC 891C 9C9B 1CC2 4363 A32B 132C для алгоритма IDEA, найти подключи четвертого раунда расшифровки. Порядок записи бит числа --- от младшего к старшему.
Отметим, что существует два способа записи бит в памяти ЭВМ: от старшего к младшему (Big-Endian) и от младшего к старшему (Little-Endian). Big-Endian использовался в ранних архитектурах ЭВМ, и для сохранения обратной совместимости остался в сетевых протоколах и некоторых форматах файлов. Little-Endian используется практически во всех современных архитектурах, поэтому мы используем его в нашей задаче.
Решение. Согласно таблице 7.10, нам нужно найти подключи 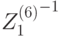 ,
,  ,
,  ,
,  ,
, 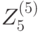 ,
, 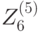 .
.
Поэтому необходимо сначала найти необходимые нам подключи для 5-го и 6-го раундов  ,
,  ,
,  ,
, 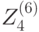 ,
, 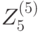 ,
, 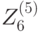 .
.
Обозначим  -й 16-битный блок ключа,
-й 16-битный блок ключа,  раз циклически сдвинутого влево на 25 бит, через
раз циклически сдвинутого влево на 25 бит, через  . Тогда данный нам исходный ключ состоит из блоков
. Тогда данный нам исходный ключ состоит из блоков 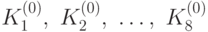 ; нужный нам подключ
; нужный нам подключ  равен некоторому блоку
равен некоторому блоку 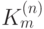 . Выпишем это соответствие, записывая индексы друг под другом:
. Выпишем это соответствие, записывая индексы друг под другом:
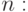 |
000000001111111122222222333333334444444455555555 |
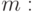 |
123456781234567812345678123456781234567812345678 |
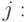 |
111111222222333333444444555555666666777777888888 |
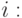 |
123456123456123456123456123456123456123456123456 |
В таблице отмечены требуемые нам подключи зашифрования. Имеем:
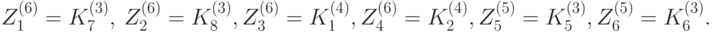
Для выполнения циклического сдвига запишем наш ключ в бинарном виде. Для этого переведём каждый шестнадцатеричный блок в двоичную систему счисления:

и выпишем блоки последовательно, начиная от младшего бита к старшему:

Для получения блока  нужно сдвинуть ключ на
нужно сдвинуть ключ на 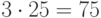 бит влево. В полученной битовой последовательности биты с 1 по 16 --- блок
бит влево. В полученной битовой последовательности биты с 1 по 16 --- блок  , c 17 по 32 --- блок
, c 17 по 32 --- блок 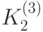 , ..., с 65 по 80 --- блок
, ..., с 65 по 80 --- блок  . Таким образом, в исходном ключе блок
. Таким образом, в исходном ключе блок  располагается с
располагается с 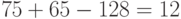 по
по 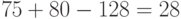 биты: 1100000111101001. Итак,
биты: 1100000111101001. Итак, 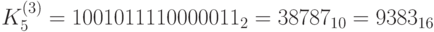 . Следующие 16 бит (0110000111000100) составляют ключ
. Следующие 16 бит (0110000111000100) составляют ключ  . Следом идут
. Следом идут 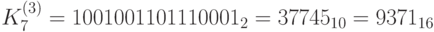 ,
, 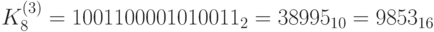 .
.
Для получения 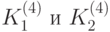 нужно сдвинуть ключ на 100 бит влево. В полученной битовой последовательности биты с 1 по 16 --- блок
нужно сдвинуть ключ на 100 бит влево. В полученной битовой последовательности биты с 1 по 16 --- блок 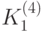 , а с 17 по 32 --- блок
, а с 17 по 32 --- блок 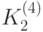 . Имеем:
. Имеем:
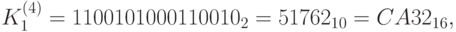
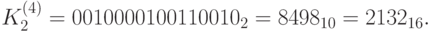
Теперь мы можем найти подключи для расшифрования:


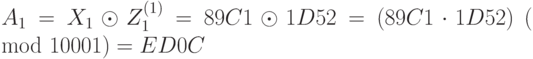 ;
;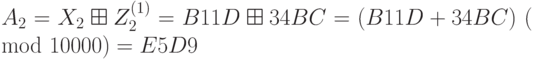 ;
;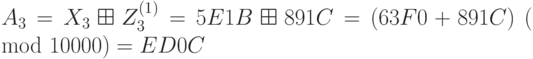 ;
;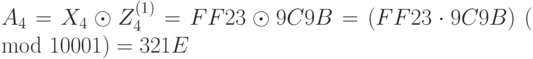 ;
; ;
; ;
;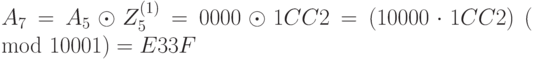 ;
; ;
;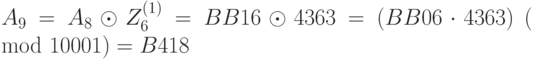 ;
; ;
;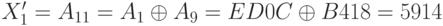 ;
;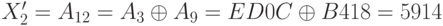 ;
; ;
; .
.