|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Современные симметричные алгоритмы шифрования
7.3.2 Дополнение. Обзор общих методов построения и тестирования блоков замен
Практически все современные блочные шифры, основанные на схеме Файстеля, содержат в числе процедур преобразования данных замену бит по специальным таблицам аналогично тому, как это делается в шифре ГОСТ 28147-89. Однако в них эти таблицы определены в спецификации алгоритма и выбираются один раз (на этапе проектирования шифра). Назначение этих таблиц (в алгоритме DES они называются S-блоками) -- перемешивание битов данных в ходе раунда шифрования путем замены отрезков шифруемого блока данных по правилам, определяемым таблицами.
Общие требования к узлам замен (S-блокам) блочных шифров повторяют требования к функции шифрования в целом -- это высокое значение нелинейности и наличие лавинного эффекта (что достигается при низком динамическом расстоянии различных порядков). Существует ряд общеизвестных критериев для проектирования устойчивых к дифференциальному криптоанализу узлов замен для любых блочных шифров:
1) Строгий критерий лавинного эффекта (SAC -- Strict Avalanche Criterion) -- требует, чтобы для любых  и
и  при инвертировании входного бита
при инвертировании входного бита  на входе узла замен выходной бит
на входе узла замен выходной бит  изменялся с вероятностью
изменялся с вероятностью 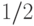 . Блок замен удовлетворяет данному критерию, если его динамическое расстояние порядка
. Блок замен удовлетворяет данному критерию, если его динамическое расстояние порядка 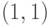 равно 0.
равно 0.
2) Критерий независимости битов (BIC -- Bit Independence Criterion) -- требует, чтобы для любых значений  ,
,  и
и  при инвертировании входного бита
при инвертировании входного бита  на входе узла замен выходные биты
на входе узла замен выходные биты  и
и  изменялись независимо (то есть вероятность одновременного изменения битов должна быть равна произведению вероятностей изменения отдельных бит). Блок замен удовлетворяет данному критерию, если динамическое расстояние порядка 1 {XOR} - суммы любых двух булевых функций, его составляющих, равно 0.
изменялись независимо (то есть вероятность одновременного изменения битов должна быть равна произведению вероятностей изменения отдельных бит). Блок замен удовлетворяет данному критерию, если динамическое расстояние порядка 1 {XOR} - суммы любых двух булевых функций, его составляющих, равно 0.
3) Критерий гарантированного лавинного эффекта (GAC -- Guaranteed Avalanche Criterion) порядка 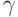 -- выполняется, если при изменении одного бита на входе узла замен на выходе меняются как минимум
-- выполняется, если при изменении одного бита на входе узла замен на выходе меняются как минимум  выходных битов.
выходных битов.
4) Критерий XOR-значения для блока  размерностью
размерностью 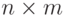 бит -- основывается на построении на основе блока специальной XOR -таблицы, элементы которой вычисляются по следующей формуле:
бит -- основывается на построении на основе блока специальной XOR -таблицы, элементы которой вычисляются по следующей формуле:

где 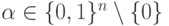 это значение может быть представлено в виде числа от
это значение может быть представлено в виде числа от  до
до 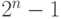 ),
), 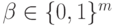 (может быть представлено в виде числа от 0 до
(может быть представлено в виде числа от 0 до 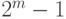 ),
), 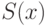 --- выходное значение блока замен
--- выходное значение блока замен  при входном значении
при входном значении  .
.
XOR-значением блока замен называется максимальное значение в его XOR-таблице. Данный критерий требует, чтобы XOR-значение блока было как можно меньшим, в идеале -- 2.
Для построения новых высокоскоростных криптоалгоритмов интерес представляют такие блока S, которые соответствуют одновременно нескольким критериям качества, и, таким образом, позволяют эффективно противостоять одновременно разным видам атак. Одними из наиболее существенных с практической точки зрения является критерий независимости векторов выхода S-блока  от векторов его входа
от векторов его входа  .
.
Более формально: обозначим через 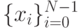 множество всевозможных входных векторов блока замен. Очевидно,
множество всевозможных входных векторов блока замен. Очевидно,  . Каждому входному вектору
. Каждому входному вектору  соответствует выходной вектор
соответствует выходной вектор  . Через
. Через 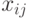 и
и  обозначим, соответственно,
обозначим, соответственно,  -й бит входного вектора и
-й бит входного вектора и  -й бит выходного вектора (
-й бит выходного вектора (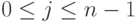 ,
,  ). Биты входных векторов
). Биты входных векторов  связаны с номером
связаны с номером  соотношением:
соотношением:

Мы также будем записывать выходной вектор 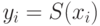 шестнадцатеричным числом, связанным с битами соотношениями:
шестнадцатеричным числом, связанным с битами соотношениями:
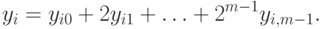
Например, если  , то
, то 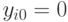 ,
,  ,
,  ,
, 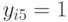 ,
, 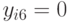 ,
, 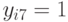 .
.
Коэффициент корреляции между  -м входным и
-м входным и  -м выходным битами узла замен вычисляется по формуле:
-м выходным битами узла замен вычисляется по формуле:
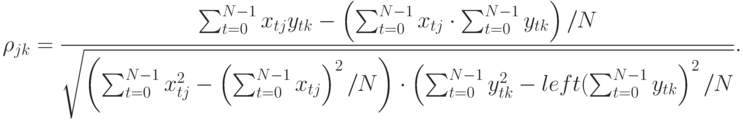
Кроме того, для двоичных векторов  ,
,  верна более простая формула:
верна более простая формула:
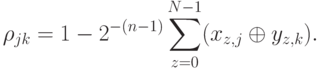 |
( 7.1) |
Пример 7.7 Вычислим коэффициенты корреляции для следующего блока замен  для алгоритма ГОСТ:
для алгоритма ГОСТ:
9 8 3 A C D 7 E 0 1 B 2 4 5 F 6
Более подробно: число 0 (нумерация начинается с нуля) переходит в число 9, число 1 переходит в 8, 2 в 3, число 3 в 10, 4 в 12,..., число 15 переходит в 6.
Запишем битовые представления всех чисел нашей подстановки:
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| 1001 | 1000 | 0011 | 1010 | 1100 | 1101 | 0111 | 1110 | 0000 | 0001 | 1011 | 0010 | 0100 | 0101 | 1111 | 0110 |
Теперь, интерпретируя последовательность битов каждого разряда как множество значений случайной величины, вычислим коэффициенты корреляции между последовательностью входящих битов  -го разряда и последовательностью выходящих битов
-го разряда и последовательностью выходящих битов  -го разряда,
-го разряда, 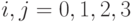 . Все коэффициенты корреляции посчитаны в таблице 7.4.
. Все коэффициенты корреляции посчитаны в таблице 7.4.
| j\k | 0 | 1 | 2 | 3 |
| 0 | -0,25 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | -0,5 |
Мы видим, что биты 1 и 2 группы остаются неизменными, что свидетельствует о плохом качестве данного блока.
Определение 7.9 Нелинейное преобразование назовем оптимальным, если все его коэффициенты корреляции равны нулю.
В работах [5], [2] представлена методика построения оптимальных блоков замен любого размера.
Существуют следующие наиболее распространенные подходы к построению блоков замен:
1) Случайный выбор. Элементы узлов замен выбираются с помощью генератора случайных или псевдослучайных чисел. Это наиболее простой способ, однако в случае небольшого размера блоков, как в алгоритме ГОСТ 28147-89 ( бит), такой способ может с высокой степенью вероятности привести к генерации таблицы замен с нежелательными с точки зрения стойкости криптостойкости характеристиками нелинейности и лавинного эффекта.
бит), такой способ может с высокой степенью вероятности привести к генерации таблицы замен с нежелательными с точки зрения стойкости криптостойкости характеристиками нелинейности и лавинного эффекта.
2) Случайный выбор с последующей проверкой. Элементы блоков замен выбираются случайным образом, но после этого полученные результаты проверяются на соответствие различным критериям с отсеиванием тех блоков, которые не выдержали такой проверки. Этот способ также прост, и в то же время он устраняет указанный недостаток первого способа, однако в таком случае встает вопрос о выборе набора критериев для проверки и формировании методики тестирования, так как не существует блоков, одинаково хорошо удовлетворяющих всем предъявляемым к ним требованиям одновременно. Также возможна ситуация, когда блоков замен, удовлетворяющим выбранным требованиям слишком мало по сравнению с мощностью пространства блоков, и генерация таких блоков на основе случайного выбора может требовать больших вычислительных ресурсов.
3) Выбор вручную. Элементы узлов замен выбираются вручную с использованием математических преобразований. Именно эта методика легла в основу разработки DES с его фиксированными S-блоками. Такой подход является наиболее сложным, так как требует разработки и теоретического обоснования методики выбора блоков замен.
4) Математический подход. Элементы узлов замен генерируются при помощи определенного алгоритма, основанного на тех или иных математических принципах. Такой подход при грамотной проектировании алгоритма обеспечивает выбор узлов замен, гарантирующих заданный уровень надежности по отношению к различным методам криптоанализа.

