Дискретизация. Антиалиасинг. Геометрические преобразования растровых изображений
Подход Веймана
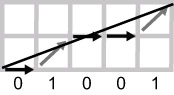
Вейманом был предложен подход [50], основанный на кодах Ротштейна (см. [46], рис. 7.18). Код Ротштейна - это бинарный код длины p, который кодирует приблизительно равномерное распределение q единиц в p разрядов. Как было показано в "Алгоритмы растеризации отрезков, окружностей и эллипсов" , это эквивалентно кодированию смещений при растеризации отрезка. Данный подход позволяет осуществлять такие преобразования, как скос и масштабирование с коэффициентами, заданными рациональными числами. С помощью комбинации этих преобразований можно представить произвольное аффинное преобразование (см. ниже).
Рассмотрим задачу масштабирования по горизонтали из изображения шириной q пикселей в изображение шириной p пикселей, p > q (т.е. коэффициент масштабирования равен p/q ). Для начала строится код Ротштейна (например, алгоритмом Брезенхема ( "Алгоритмы растеризации отрезков, окружностей и эллипсов" )). Наиболее просто скопировать q исходных колонок в те колонки, которые помечены кодом 1. Но это приведет к пробелам в тех столбцах, где значение кода равно 0. Поэтому данное распределение по колонкам применяется к циклическим перестановкам кода Ротштейна; при этом происходит суммирование в каждой колонке, а затем результат усредняется (делится на q, т.к. всего было p циклических перестановок и каждая колонка была закрашена q раз).
Для случая сжатия (когда p < q ) строится код длины q, и теперь уже, наоборот, 1 -цы соответствуют выбору тех исходных столбцов, которые копируются в результирующие p. Аналогично, с целью устранения алиасинга, результат усредняется по всем циклическим перестановкам кода (деление снова на q, т.к. прибавка к каждой колонке происходит при каждой перестановке).
// q - исходная ширина, p - ширина результата (p > q)
// I0 - исходное изображение (q x n)
// I1 - результирующее изображение (p x n)
I1 = 0; // установим все пиксели в I1 равными 0
code = ComputeCode( p, q ); // код длины p
// по всем циклическим перестановкам
foreach( perm in 1...p )
{
code = CyclicShift( code );
srcI = 0;
foreach( dstI in 1...p )
if( code[dstI] == 1 )
{
foreach( J in 1...p )
I1(dstI,J) += I0(srcI,J);
srcI++;
}
}
// усредняем
foreach( pixel in I1 )
I1(pixel) = I1(pixel) / q;
Листинг
7.3.
Алгоритм Веймана для растяжения по горизонтали
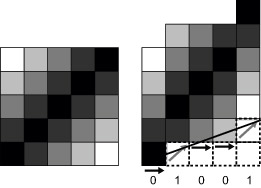
Для вертикального скоса с коэффициентом p/q < 1 применяется модификация, где 1 в коде указывает на то, что текущий столбец следует сдвинуть вверх на 1 пиксель (см. рис. 7.19). Так же, как и для растяжения, с целью фильтрации результат усредняется по циклическим перестановкам кода.