Дискретизация. Антиалиасинг. Геометрические преобразования растровых изображений
7.2. Антиалиасинг
Антиалиасинг или Фильтрация-сглаживание (англ. antialiasing) - устранение видимых артефактов дискретизации, особенно для изображений линий или краев объектов. Возможны два основных подхода.
- Учет эффектов дискретизации в алгоритмах построения изображений. То есть, фактически, встраивание в них префильтрации.
- Адаптивная дискретизация с постфильтрацией. Получение нового дискретизированного изображения по другому дискретизированному с помощью дискретной фильтрации, т.н. постфильтрации. Данный подход может быть эффективен при переходе от промежуточной большей частоты дискретизации к меньшей. Процесс растеризации с увеличенной по отношению к требуемой частотой первичной дискретизации с последующей постфильтрацией называется супердискретизацией (англ. supersampling). Первичная частота дискретизации может варьироваться в разных частях изображения в зависимости от его свойств.
Растеризация с антиалиасингом
При растеризации абстрактно определенных примитивов (точек, линий, многоугольников) можно рассматривать их как двумерный сигнал и применить к нему префильтрацию как описано в предыдущем разделе. В "Основные понятия. Представление цвета в машинной графике" в качестве одной из моделей понятия растра рассматривалось замощение плоскости, где каждый пиксель представляет собой квадрат. При растеризации этому квадрату нужно приписать цвет так, чтобы при взгляде на изображение растра на каком-либо устройстве вывода воспринимаемая картинка была наиболее похожа на исходный непрерывный двумерный сигнал.
Заметим, что выражение (7.8) линейно по Img и, следовательно, обладает свойством суперпозиции по отношению к Img. Т.е. если Img состоит из нескольких непересекающихся объектов, то в (7.8) достаточно будет просуммировать вклад от этих объектов. Конечно, надо оговориться, что это возможно только в том случае, если атрибут пикселя принимает достаточное количество значений (для монохромных изображений антиалиасинг неприменим). Для цветных изображений проводимые рассуждения справедливы для каждого канала.
Понятно, что с увеличением радиуса фильтра изображение будет все более сглаженным и даже размытым, а с уменьшением радиуса уменьшится его эффект для антиалиасинга.
В данном разделе мы ограничимся лишь растеризацией базовых объектов - отрезков и общих кривых. Впрочем, подобные методы с незначительными модификациями применимы для антиалиасинга краев (которые также являются отрезками или общими кривыми) более сложных объектов (см., например, [29]).
Алгоритм Гупты-Спрулла
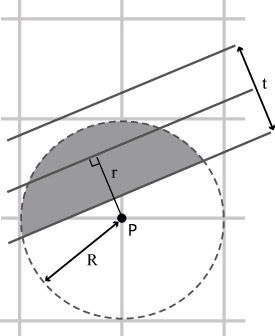
Данный алгоритм для растеризации отрезков с целочисленными координатами концов был предложен Гуптой и Спруллом в статье [34]. В нем предполагается использование радиально-симметричного фильтра (такого как конический). Пусть его радиус равен R. Для того чтобы выяснить, каким цветом следует закрасить пиксель, необходимо посчитать значение свертки фильтра с функцией прямой ( I = 1 в вытянутом прямоугольнике толщиной t и 0 вне него), см. рис. 7.11. Обозначим результат этой операции FR,t(r), где r - расстояние от центра закрашиваемого пикселя до центральной оси прямой. Заметим, что FR,t(r) = 0 для r > R + t/2.
Идея алгоритма состоит в модификации алгоритма Брезенхема (
"Алгоритмы растеризации отрезков, окружностей и эллипсов"
) для одновременной закраски нескольких пикселей разной интенсивности в столбце (см. рис. 7.12). Так же, как и в алгоритме Брезенхема, речь идет о случае наклона прямой меньше чем на 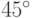 . Случай вертикального наклона аналогично просто сводится к первому случаю (
"Алгоритмы растеризации отрезков, окружностей и эллипсов"
).
. Случай вертикального наклона аналогично просто сводится к первому случаю (
"Алгоритмы растеризации отрезков, окружностей и эллипсов"
).
Количество пикселей, которые могут быть закрашены в одном столбце зависит от t и R, а также от наклона прямой. Канонически будем полагать радиус фильтра R = 1 и толщину отрезка t = 1. Тогда максимально может быть закрашено 4 пикселя при наклоне, близком к 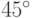 . Если рассматривать конический фильтр, то в случае 4 пикселей возможный вклад самого верхнего или нижнего будет достаточно мал, поэтому для упрощения алгоритма будем закрашивать только ближайшие 3 к пересечению прямой с вертикалью пикселя.
. Если рассматривать конический фильтр, то в случае 4 пикселей возможный вклад самого верхнего или нижнего будет достаточно мал, поэтому для упрощения алгоритма будем закрашивать только ближайшие 3 к пересечению прямой с вертикалью пикселя.
Пусть, как и в
"Алгоритмы растеризации отрезков, окружностей и эллипсов"
, строится отрезок  .
.
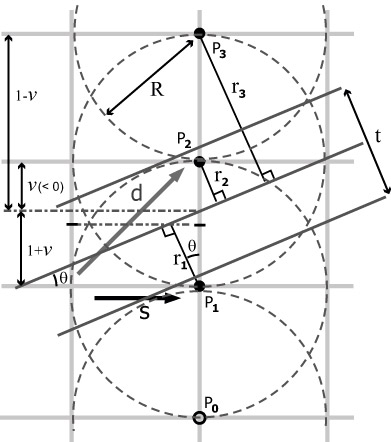
Обозначим нижний текущий (как в алгоритме Брезенхема) пиксель P2, нижний - P1, а верхний - P3 (см. рис. 7.12). Пусть v - расстояние от центральной точки между рассматриваемыми пикселями до выбранного пикселя P2. Оно может быть как положительным (если выбран шаг s ), так и отрицательным (если выбран шаг d ). Тогда соответствующие расстояния до оси прямой равны
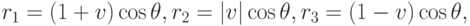
где  равен углу наклона прямой (см. рис. 7.12), т.е.
равен углу наклона прямой (см. рис. 7.12), т.е. 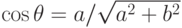 .
.
Если обратиться к исходному алгоритму Брезенхема ( "Алгоритмы растеризации отрезков, окружностей и эллипсов" ), несложно заметить, что
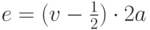
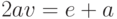 . Тогда
. Тогда 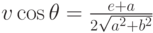 .
.Для ускорения вычислений построим дискретную аппроксимацию FR,t(r), разбив интервал [0,R + t/2] на равные части и аппроксимируя значение F в каждом интервале значением в центре этого интервала. Получим таблицу значений интенсивности ITable.
Пусть функция round находит номер интервала по действительному значению в [0,R + t/2]. Тогда, модифицируя алгоритм Брезенхема, получаем следующий алгоритм:
// plot(x,y,I) закрашивает пиксель (x,y) с интенсивностью I
e = 2b - a;
Delta eS = 2b;
Delta eD = 2b - 2a;
denom = 1/(2*sqrt(a*a+b*b));
fixPart = 2a*denom; // фикс. часть r_1 и r_3
// (x,y) - Координаты текущей точки
x= 0; y = 0;
while( x < a )
{
av2 = (e+a)*denom;
plot(x, y-1, ITable[round(fixPart+av2)] );
plot(x, y, ITable[round(abs(av2))] );
plot(x, y+1, ITable[round(fixPart-av2)] );
if( e > 0 )
{
// d : диагональное смещение
x++; y++;
e += Delta eD;
}
else
{
// s : горизонтальное смещение
x++;
e += Delta eS;
}
}
Листинг
7.1.
Алгоритм Гупты-Спрулла для отрезка
Конечно, еще желательно специально обрабатывать начало и конец отрезка, но подробное обсуждение этого выходит за рамки данной книги. Подробности можно узнать в [34].