Заполнение многоугольников и областей
6.1. Введение
В предыдущих лекциях мы рассмотрели алгоритмы отображения линий на растре. Линии на растре зачастую образуют замкнутые области, которые требуется закрасить (заполнить) тем или иным цветом. В этой лекции мы рассмотрим алгоритмы, позволяющие выполнить такое заполнение.
Будут рассмотрены два случая. В первом требуется нарисовать на растре многоугольник, заданный своими вершинами ( растеризация многоугольника ). Во втором, более общем случае мы будем считать, что растровая область задана цветом своей границы и точкой (пикселем) внутри области. Этот пиксель называется затравочным, а сам метод называется заполнением с затравкой.
6.2. Растеризация многоугольников
Пусть задан многоугольник P1P2 . . . PNP1 и требуется растеризовать его вместе с внутренними точками. Будем считать, что процедура отсечения (
"Отсечение отрезков и многоугольников"
) при необходимости была уже произведена и многоугольник целиком помещается в растровом окне. Для удобства каждое ребро многоугольника будем задавать координатами (x1, y1) и (x2, y2)
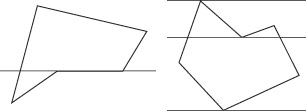
его концов, так, что  . Условимся также отсчитывать на экране координату x слева направо, а y - сверху вниз (таким образом, точка (x1, y1) будет верхним концом ребра, а (x2, y2) - нижним). Большинство алгоритмов заполнения основано на том факте, что любое горизонтальное сечение контура многоугольника состоит из четного числа точек. Это утверждение неверно в двух случаях (см. рис. 6.1):
. Условимся также отсчитывать на экране координату x слева направо, а y - сверху вниз (таким образом, точка (x1, y1) будет верхним концом ребра, а (x2, y2) - нижним). Большинство алгоритмов заполнения основано на том факте, что любое горизонтальное сечение контура многоугольника состоит из четного числа точек. Это утверждение неверно в двух случаях (см. рис. 6.1):
- когда секущая прямая содержит горизонтальное ребро;
- когда она содержит вершину, а оба смежных ребра лежат выше (ниже) ее.
Однако существуют простые способы исключить эти случаи из рассмотрения; они будут рассмотрены позднее. Пока же будем считать, что приведенное утверждение справедливо всегда. Задача заполнения многоугольника, таким образом, сводится к заполнению определенных промежутков между точками сечения, что должно быть проделано для каждого горизонтального сечения многоугольника. Заметим, что при таком подходе никаких ограничений на свойства многоугольника (выпуклость, отсутствие самопересечений и т.д.) не накладывается.
Алгоритм со списком реберных точек
Этот алгоритм состоит из трех основных этапов.
На первом этапе растеризуются все негоризонтальные ребра многоугольника. Все точки помещаются в списки. Для каждой координаты ymin, y2 . . . ymax сопоставим список x-координат всех пикселей, закрашенных при растеризации ребер, которые находятся на горизонтали y (здесь ymin и ymax - минимальная и максимальная y-координаты пикселей в растровом изображении многоугольника). Формально процедура описывается так:
foreach( ребро (x1, y1) - (x2, y2) in МножествоРебер )
{
y = ceil(y1); // Округление до большего
dx = (x2 - x1)/(y2 - y1);
x = x1 + dx*(y - y1);
while(y <= y2)
{
PutToList(x, y); // поместить x в список,
// соответствующий данному y
y++;
x += dx;
}
}
Листинг
6.1.
Растеризация ребер
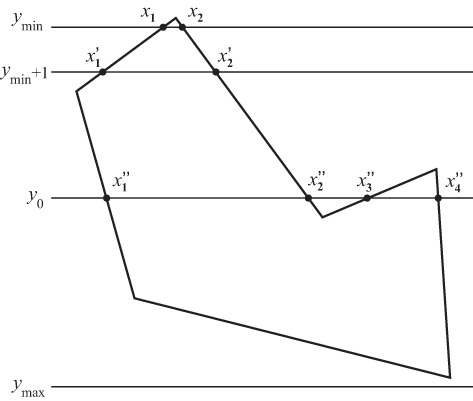
На втором этапе для каждого y списки упорядочиваются по возрастанию. После этого для многоугольника, изображенного на рис. 6.2, списки будут выглядеть следующим образом:
На третьем этапе в каждой строке заполняются все отрезки вида [x2i-1, x2i].