Дискретизация. Антиалиасинг. Геометрические преобразования растровых изображений
Теорема Найквиста-Котельникова
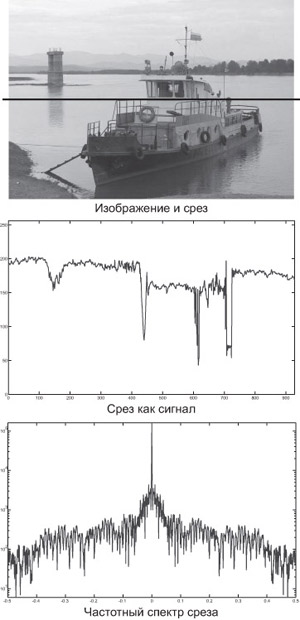
Теорема Найквиста-Котельникова дает ответ на вопрос, какой частоты дискретизации fs достаточно для того, чтобы не произошло потери информации, т.е. чтобы по дискретизованному сигналу можно было восстановить исходный. Применительно к изображениям это грубо (поскольку еще не ясно, как происходит восстановление, которое зависит от устройства отображения) можно понимать так: "Какая разрешающая способность должна быть у растра, чтобы он сохранил все детали исходного аналогового изображения". Хотя потеря информации даже в случае соблюдения условий теоремы Котельникова произойдет из-за того, что значения дискретизованной функции (растрового изображения) в компьютере сами хранятся с ограниченной точностью. Передача цветов и оттенков лучшим образом при ограниченном диапазоне значений является задачей квантования, которая рассмотрена в "Алгоритмы квантования для полутоновых и цветных изображений" .
В доказательстве теоремы и далее будет использоваться операция свертки функций I(x), J(x), определяемая так:
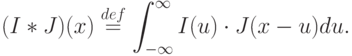
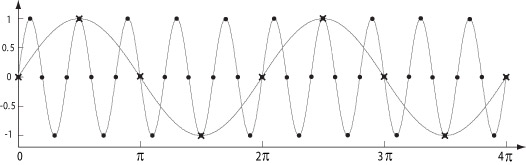
Теорема 7.1.1 (Найквиста-Котельникова). Для того чтобы сигнал I(x) можно было восстановить по его дискретному образу, его спектр должен быть ограничен максимальной частотой fH и частота дискретизации fs должна быть более 2fH.
Доказательство использует факты из математического и функционального анализа (см. например [3]). Пусть Is(x) - дискретный образ исходного сигнала I(x), как обычно, T = 1/fs - период дискретизации, тогда
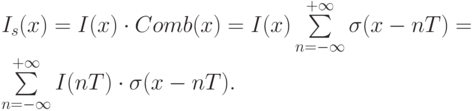
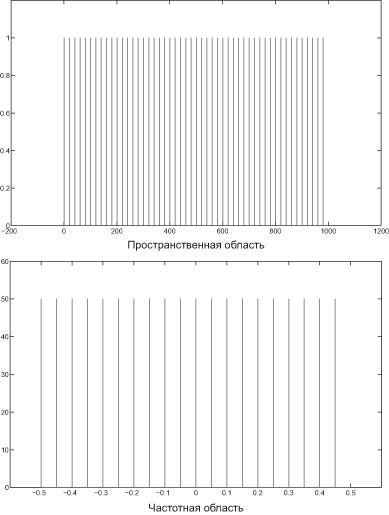
Образом функции Comb в частотной области является функция
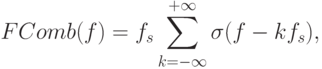
а Фурье-образ I(x) по-прежнему будем обозначать F(f). Умножение функций в пространственной области соответствует их свертке (будем обозначать ее  ) в частотной и наоборот. Соответственно, рассмотрим свертку F и FComb, являющуюся Фурье-образом Is(x) (обозначим его Fs(f) ):
) в частотной и наоборот. Соответственно, рассмотрим свертку F и FComb, являющуюся Фурье-образом Is(x) (обозначим его Fs(f) ):
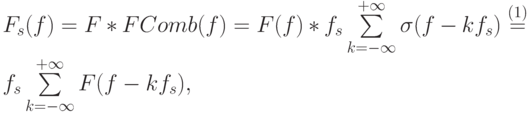 |
( 7.6) |
где переход (1) произошел благодаря сдвигающему свойству дельта-функции при свертке. Как видно из последнего выражения, Fs(f) представляет собой бесконечную сумму функций F(f), умноженных на fs и сдвинутых на fs относительно друг друга, поэтому при условии fs > 2fH носители соседних сдвинутых версий не пересекаются, и отдельно, взяв центральную копию F(f) (k = 0) и применив к ней обратное преобразование Фурье, можно получить исходный сигнал I(x). Центральная копия берется путем умножения Fs(f) на прямоугольную функцию 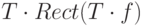 , где
, где
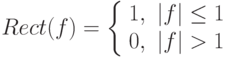
Т.е. 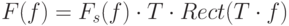 , - образ исходной функции получен. Заметим, этому умножению в частотной области соответствует свертка в пространственной области. Применив обратное преобразование Фурье к
, - образ исходной функции получен. Заметим, этому умножению в частотной области соответствует свертка в пространственной области. Применив обратное преобразование Фурье к 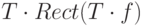 , получим функцию
, получим функцию
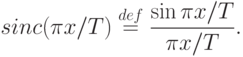 |
( 7.7) |
Применив свертку с Is(x), получаем
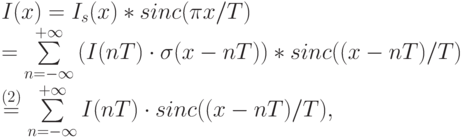
где переход (2) также произошел благодаря сдвигающему свойству дельта-функции при свертке. Последняя формула называется Интерполяционной формулой Найквиста-Шеннона.
Для завершения доказательства осталось показать, что невозможно однозначно восстановить сигнал при 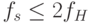 .
.
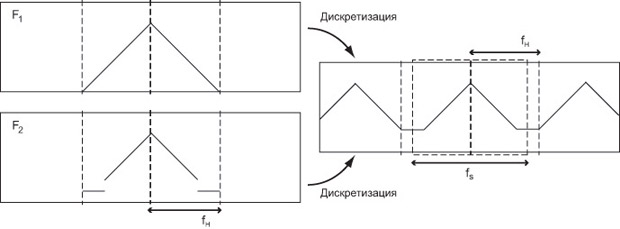
Приведем соответствующий пример. Зафиксируем две частоты - fs и fH, 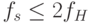 ; для упрощения рассуждений предположим, что fs > fH (в общем случае может быть более двух наложений сдвинутых образов, что усложнит построение контрпримера). Из формулы (7.6) следует, что Фурье-образ Is(x) является периодической функцией с периодом fs, поэтому вся информация для восстановления содержится в одном периоде (например
; для упрощения рассуждений предположим, что fs > fH (в общем случае может быть более двух наложений сдвинутых образов, что усложнит построение контрпримера). Из формулы (7.6) следует, что Фурье-образ Is(x) является периодической функцией с периодом fs, поэтому вся информация для восстановления содержится в одном периоде (например ![f \in [-\frac{f_s}{2}, \frac{f_s}{2}]](/sites/default/files/tex_cache/6423933812d3322af6aef5d4689221f9.png) ). Рассмотрим две функции, Фурье-образы которых равны
). Рассмотрим две функции, Фурье-образы которых равны
![F_1(f) =\left\{ \begin{array}{ccc}
f_H - |f|, & |f| \in [0, f_s - f_H) \\
\frac{2f_H-f_s}{2}, & |f| \in [f_s - f_H, f_H] \\
0, & |f| > f_H \\
\end{array} \right.](/sites/default/files/tex_cache/4448bc4792b9968e5a6987ef00b3b852.png)
![F_2(f) = \left\{ \begin{array}{cc}
f_H - |f|, & |f| \in [0, f_H] \\
0, & |f| > f_H \\
\end{array} \right.](/sites/default/files/tex_cache/f77e7587597e0bc5949e85d49d0ef7c3.png)
(функция однозначно задается своим Фурье-образом). При дискретизации с частотой fs в соответствии с формулой (7.6) Фурье-образ в интервале ![[-\frac{f_s}{2}, \frac{f_s}{2}]](/sites/default/files/tex_cache/78a7bd382dabd19c7e1982e68c9a6ad3.png) для обеих функций будет равен
для обеих функций будет равен
![F_s(f) = \left\{ \begin{array}{cc}
f_s(f_H - |f|), & |f| \in [0, f_s - f_H) \\
f_s(2f_H - f_s), & |f| \in [f_s - f_H, f_s/2] \\
\end{array} \right.](/sites/default/files/tex_cache/3e7266cd914aec6a6ef4bce4dd224a52.png)
Таким образом, в этом случае однозначная реконструкция невозможна.