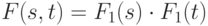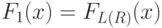Дискретизация. Антиалиасинг. Геометрические преобразования растровых изображений
| Название | Функция фильтра F(x) |
|---|---|
| Импульсный (pulse) |
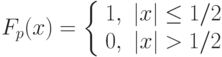 |
| Треугольный (triangle) | 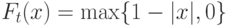 |
| Гауссовский (Gaussian) |
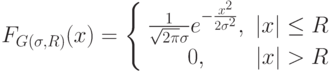 |
| Кубический (cubic) |
 |
| Ланцоша (Lanzcos) |
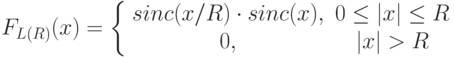 |
Двумерные аналоги одномерного фильтра f11(x) строятся двумя путями:
- как функция от радиуса:
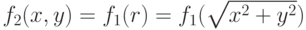 ;
; - как произведение:
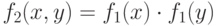 .
.
Первый вариант - более корректный, но второй обладает свойством сепарабельности, т.е. в выражении (7.8) можно двумерное интегрирование разбить на два одномерных:
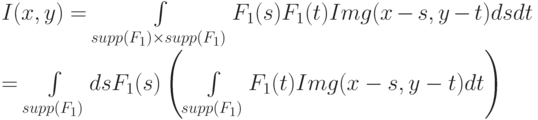
Как будет показано в разделе 7.3, в случае передискретизации интегрирование заменяется суммированием и в этом случае быстрее производить вычисления в два этапа, каждый из которых состоит в дискретной свертке по одному измерению и может быть вычислен достаточно эффективно (в том числе и с применением параллельных алгоритмов). В алгоритмах растеризации с префильтрацией более популярны фильтры первого типа, а для геометрических преобразований, где происходит передискретизация - второго.
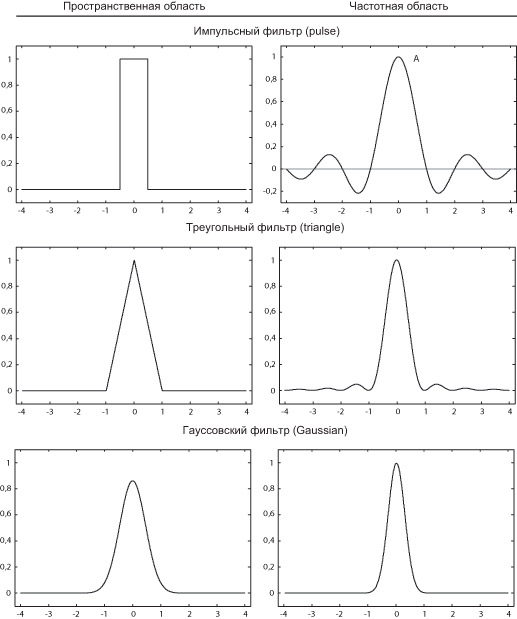
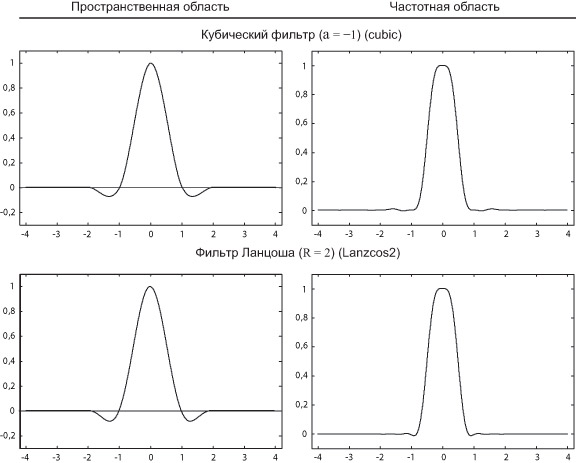
Двумерные аналоги фильтров, представленных в таблице 7.1 и на рис. 7.9 и 7.10, приведены в таблицах 7.2, 7.3 (для простоты частота дискретизации равна 1, произвольный случай получается масштабированием по осям). Прямоугольный фильтр соответствует либо цилиндру (первый тип), либо параллелепипеду с квадратным основанием (англ. Box filter) (второй тип); треугольный соответствует либо конусу, либо пирамиде соответственно. По смыслу прямоугольные и треугольные аналоги соответствуют так называемым невзвешенной и взвешенной площадным выборкам. Если рассмотреть Фурье-образы их одномерных аналогов на рис. 7.9, можно заметить, что взвешенная площадная выборка лучше отфильтровывает высокие частоты, поэтому рекомендуется применять именно ее.
| Название | Функция фильтра  ( ( 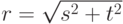 ) ) |
Изображение |
|---|---|---|
| Цилиндрический |  |
|
| Конусообразный |  |
|
| Кубический | 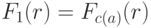 |
|
| Ланцоша |  |
Проблема растеризации с учетом антиалиасинга рассмотрена в разделе 7.2. В разделе 7.3 рассмотрены проблемы получения дискретных изображений по другим дискретным изображениям.