Дискретизация. Антиалиасинг. Геометрические преобразования растровых изображений
7.3. Геометрические преобразования растровых изображений
Построение дискретного изображения, которое было подвергнуто геометрическому преобразованию, при условии наличия дискретизации исходного изображения является фактически проблемой передискретизации.
Пусть исходное (непрерывное) изображение задано функцией I(x, y), тогда его дискретизация Is(x, y) (считаем частоту равной fs ) будет получена умножением на функцию двумерной "решетки":

Следовательно, мы получили растр, с атрибутами
 |
( 7.11) |
Пусть преобразование задано функцией 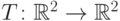 :
:
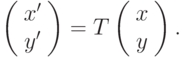
Тогда преобразованное изображение равно I'(x', y') = I(T-1(x', y')), дискретизация (c частотой f's ) преобразованного изображения должна быть получена как
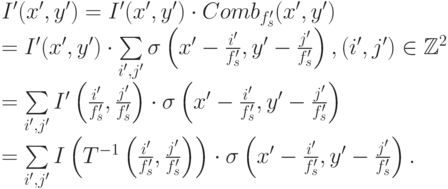 |
( 7.12) |
Мы рассматриваем задачу, когда нам неизвестно исходное изображение, а известна только его дискретизация Is. В таком случае в качестве I в (7.12) следует подставить реконструированное изображение Ir. Реконструкция производится с помощью реконструирующего фильтра RFilter:
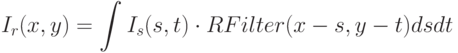 |
( 7.13) |
 |
( 7.14) |
В идеальном случае, когда начальная частота дискретизации была больше частоты Найквиста и в качестве RFilter выступает функция sinc изображение будет реконструировано точно, т.е. Ir = I. На практике же в качестве RFilter выступают различные аппроксимации sinc с локальным носителем (см. таблицу 7.1), что дает некоторые искажения (в частности, размытие).
Если в выражение (7.12) подставить Ir, вычисленное по формуле (7.14) вместо I и воспользоваться определением (7.11) для атрибутов нового растра I's(i', j') то получаем, что
 |
( 7.15) |
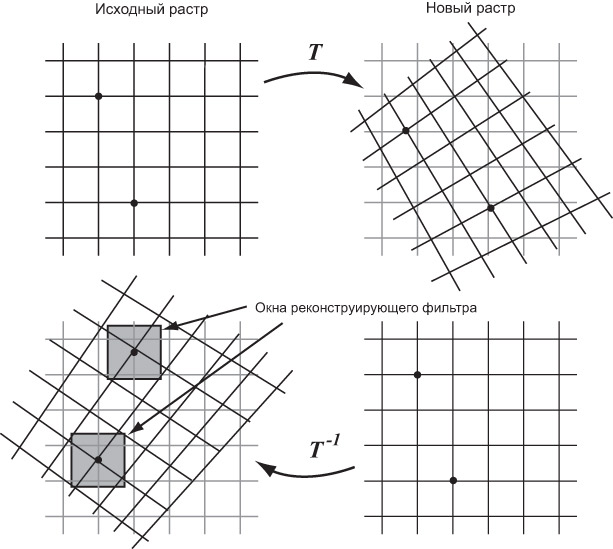
Таким образом, задача передискретизации сводится к применению дискретной свертки (фактически суммированию) исходного дискретизованного изображения Is с функцией фильтра RFilter, центрированной в прообразе нового пикселя при преобразовании T (см. рис. 7.15).
Линейные фильтры, используемые в качестве RFilter, фактически осуществляют локальную интерполяцию или аппроксимацию поверхности Ir по точкам дискретизации. Если мы просто будем считать Ir некоторой поверхностью, то в этом случае
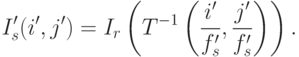
Если в качестве фильтра выступает функция-параллелепипед, то при передискретизации новое значение будет просто средним по пикселям, попавшим в область носителя (для малого радиуса ( 1/2 ) - просто значение ближайшего пикселя). Пирамидальному фильтру соответствует билинейная интерполяция. Более качественные результаты можно получить при использовании бикубической интерполяции, которая соответствует сепарабельному кубическому фильтру (см. таблицу 7.3). Она является стандартной в популярном растровом редакторе Adobe Photoshop.
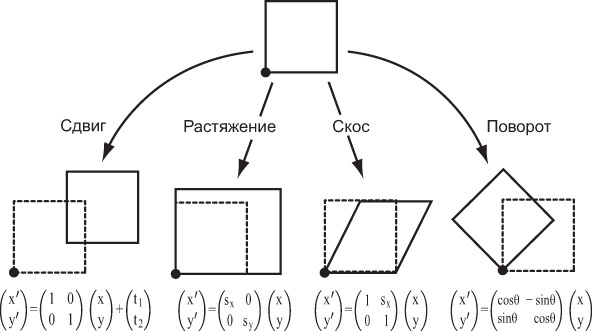
Предметом нашего рассмотрения будут в основном аффинные преобразования:
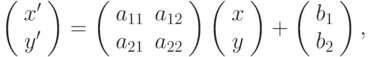
частным случаем которых являются сдвиги, растяжения, скосы и повороты (см. рис. 7.16).
В трехмерной графике подобные проблемы возникают при текстурировании, т.е. наложении искаженных растровых изображений на поверхности объектов, которые затем проецируются на экран. Там, как правило, речь идет о перспективных преобразованиях (задаются невырожденной трехмерной матрицей  ):
):
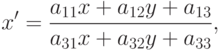
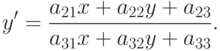
При перспективных преобразованиях возможны значительные искажения, при которых эффективная частота дискретизации, обратно пропорциональная расстоянию между переведенными точками  , может быть значительно больше исходной, которая полагается равной 1 (в пикселях исходного изображения). В этом случае прибегают к супердискретизации. Локально для
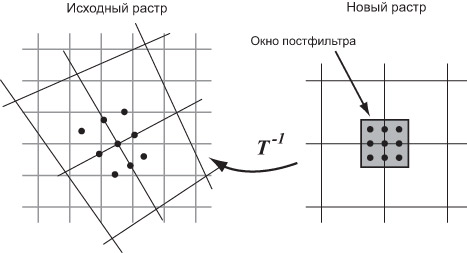
одного пикселя в I' строится промежуточная дискретизация с частотой, большей чем f' (обычно в целое число раз, которое зависит от степени искажения3Вопрос о том, как приблизительно вычислить это число, выходит за рамки данной книги. Довольно хорошо разработан данный вопрос для задач текстурирования. ), а затем по ней с помощью второго этапа дискретной фильтрации (зачастую здесь применяется простейший усредняющий фильтр-параллелепипед) получаем значение интенсивности результирующего пикселя (см. рис. 7.17). Более подробно о супердискретизации можно узнать из литературы, посвященной текстурированию.
, может быть значительно больше исходной, которая полагается равной 1 (в пикселях исходного изображения). В этом случае прибегают к супердискретизации. Локально для
одного пикселя в I' строится промежуточная дискретизация с частотой, большей чем f' (обычно в целое число раз, которое зависит от степени искажения3Вопрос о том, как приблизительно вычислить это число, выходит за рамки данной книги. Довольно хорошо разработан данный вопрос для задач текстурирования. ), а затем по ней с помощью второго этапа дискретной фильтрации (зачастую здесь применяется простейший усредняющий фильтр-параллелепипед) получаем значение интенсивности результирующего пикселя (см. рис. 7.17). Более подробно о супердискретизации можно узнать из литературы, посвященной текстурированию.
Как всегда, на практике, пожертвовав точностью, можно получить более быстродействующие алгоритмы.