Двунаправленная ассоциативная память
Память человека часто является ассоциативной; один предмет напоминает нам о другом, а другой — о третьем. Если выпустить наши мысли из-под контроля, они будут перемещаться от предмета к предмету по цепочке умственных ассоциаций. Кроме того, возможно использование ассоциативного мышления для восстановления забытых образов. Если мы забыли, где оставили свои очки, то пытаемся вспомнить, где видели их в последний раз, с кем в это время разговаривали и что делали. Так устанавливается конец цепочки ассоциаций, и это позволяет нашей памяти соединять ассоциации для получения требуемого образа.
Ассоциативная память, рассмотренная в предыдущих лекциях, является, строго говоря, автоассоциативной: это означает, что образ может быть завершен или исправлен, но не может быть ассоциирован с другим образом. Данный факт является результатом одноуровневой структуры ассоциативной памяти, в ней вектор появляется на выходе тех же нейронов, на которые поступает входной вектор.
Двунаправленная ассоциативная память (ДАП) является гетероассоциативной; входной вектор поступает на один набор нейронов, а соответствующий выходной вектор появляется на другом наборе нейронов. Как и сеть Хопфилда, ДАП способна к обобщению, вырабатывая правильные реакции, несмотря на искаженные входы. Кроме того, могут быть реализованы адаптивные версии ДАП, выделяющие эталонный образ из зашумленных экземпляров. Эти возможности сильно напоминают процесс мышления человека и позволяют искусственным нейронным сетям приблизиться к моделированию естественного мозга.
Структура ДАП
На рис. 10.1 приведена базовая конфигурация ДАП. Она
выбрана таким образом, чтобы подчеркнуть сходство с сетями Хопфилда и
предусмотреть увеличения количества слоев. На рис. 10.1 входной
вектор  обрабатывается матрицей весов
обрабатывается матрицей весов  сети, в
результате чего
вырабатывается вектор выходных сигналов нейронов
сети, в
результате чего
вырабатывается вектор выходных сигналов нейронов 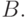 Вектор
Вектор  затем
обрабатывается транспонированной матрицей
затем
обрабатывается транспонированной матрицей 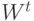 весов сети, которая
вырабатывает новые выходные сигналы, представляющие собой новый
входной вектор
весов сети, которая
вырабатывает новые выходные сигналы, представляющие собой новый
входной вектор 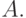 Процесс повторяется до тех пор, пока сеть не
достигнет
стабильного состояния, в котором ни вектор
Процесс повторяется до тех пор, пока сеть не
достигнет
стабильного состояния, в котором ни вектор  , ни вектор
, ни вектор  не
изменяются. Заметим, что нейроны в слоях 1 и 2 функционируют, как и в
других парадигмах, вычисляя сумму взвешенных входов и вычисляя по ней
значение функции активации
не
изменяются. Заметим, что нейроны в слоях 1 и 2 функционируют, как и в
других парадигмах, вычисляя сумму взвешенных входов и вычисляя по ней
значение функции активации 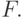 Этот процесс может быть выражен
следующим образом:
Этот процесс может быть выражен
следующим образом:
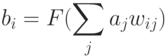
или в векторной форме:

где  — вектор выходных сигналов нейронов слоя 2,
— вектор выходных сигналов нейронов слоя 2,  — вектор
выходных сигналов нейронов слоя 1,
— вектор
выходных сигналов нейронов слоя 1,  — матрица весов связей
между
слоями 1 и 2,
— матрица весов связей
между
слоями 1 и 2,  — функция активации.
— функция активации.
Аналогично,
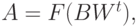
где 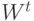 является транспозицией матрицы
является транспозицией матрицы 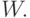
Как отмечено нами ранее, Гроссберг показал преимущества использования сигмоидальной (логистической) функции активации

где 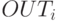 — выход нейрона
— выход нейрона  ,
, 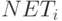 — взвешенная сумма входных
сигналов нейрона
— взвешенная сумма входных
сигналов нейрона  ,
,  — константа,
определяющая степень
кривизны.
— константа,
определяющая степень
кривизны.
В простейших версиях ДАП значение
константы  выбирается большим, в результате чего функция активации приближается к
простой пороговой функции. В дальнейшем будем предполагать, что
используется пороговая функция активации.
выбирается большим, в результате чего функция активации приближается к
простой пороговой функции. В дальнейшем будем предполагать, что
используется пороговая функция активации.
Примем также, что существует память внутри каждого нейрона в слоях 1 и 2 и что выходные сигналы нейронов изменяются одновременно с каждым тактом синхронизации, оставаясь постоянными в паузах между этими тактами. Таким образом, поведение нейронов может быть описано следующими правилами:

где 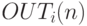 представляет собой величину выходного сигнала
нейрона
представляет собой величину выходного сигнала
нейрона  в момент времени
в момент времени 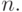
Заметим, что, как и в описанных ранее сетях, слой 0 не производит
вычислений и не имеет памяти ; он
является только средством
распределения выходных сигналов слоя 2 к элементам матрицы 

