Процедура обратного распространения (описание алгоритма)
Введение в процедуру обратного распространения
Среди различных структур нейронных сетей (НС) одной из наиболее известных является многослойная структура, в которой каждый нейрон произвольного слоя связан со всеми аксонами нейронов предыдущего слоя или, в случае первого слоя, со всеми входами НС. Такие НС называются полносвязными. Когда в сети только один слой, алгоритм ее обучения с учителем довольно очевиден, так как правильные выходные состояния нейронов единственного слоя заведомо известны и подстройка синаптических связей идет в направлении, минимизирующем ошибку на выходе сети. По этому принципу строится, например, алгоритм обучения однослойного персептрона. В многослойных же сетях оптимальные выходные значения нейронов всех слоев, кроме последнего, как правило, не известны, и двух- или более слойный персептрон уже невозможно обучить, руководствуясь только величинами ошибок на выходах НС.
Один из вариантов решения этой проблемы — разработка наборов выходных сигналов, соответствующих входным, для каждого слоя НС, что, конечно, является очень трудоемкой операцией и не всегда осуществимо. Второй вариант — динамическая подстройка весовых коэффициентов синапсов, в ходе которой выбираются, как правило, наиболее слабые связи и изменяются на малую величину в ту или иную сторону, а сохраняются только те изменения, которые повлекли уменьшение ошибки на выходе всей сети. Очевидно, что данный "метод тыка", несмотря на свою кажущуюся простоту, требует громоздких рутинных вычислений. И, наконец, третий, более приемлемый вариант — распространение сигналов ошибки от выходов НС к ее входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Этот алгоритм обучения НС получил название процедуры обратного распространения. Разработка алгоритма обратного распространения сыграла важную роль в возрождении интереса к искусственным нейронным сетям. Обратное распространение — это систематический метод для обучения многослойных искусственных нейронных сетей. Он имеет солидное математическое обоснование. Несмотря на некоторые ограничения, процедура обратного распространения сильно расширила область проблем, в которых могут быть использованы искусственные нейронные сети, и убедительно продемонстрировала богатые возможности этой методики.
Обучающий алгоритм обратного распространения
Сетевые конфигурации:
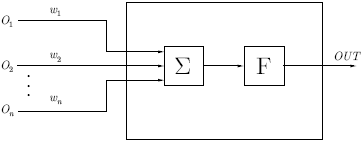
Нейрон. На рис. 4.1 показан нейрон, используемый в качестве основного строительного блока в сетях обратного распространения. Подается множество входов, идущих либо извне, либо от предшествующего слоя. Каждый из них умножается на вес, и произведения суммируются:
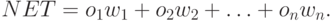
Эта сумма, обозначаемая 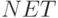 , должна быть вычислена для каждого
нейрона сети. После того, как величина
, должна быть вычислена для каждого
нейрона сети. После того, как величина 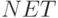 вычислена, она
модифицируется с помощью активационной функции, и получается сигнал OUT. Для алгоритмов
обратного распространения обычно используется функция
вычислена, она
модифицируется с помощью активационной функции, и получается сигнал OUT. Для алгоритмов
обратного распространения обычно используется функция
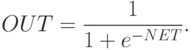 |
( 1) |
Как показывает уравнение (1), эта функция, называемая сигмоидом, весьма удобна, так как имеет простую производную, что используется при реализации алгоритма обратного распространения:
 |
( 2) |
Сигмоид, который иногда называется также логистической или сжимающей функцией,
сужает диапазон изменения 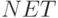 так, что значение
так, что значение 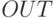 лежит между нулем и единицей. Как указывалось выше, многослойные нейронные
сети обладают большей представляющей мощностью,
чем однослойные, лишь в случае присутствия нелинейности. Сжимающая
функция обеспечивает требуемую нелинейность.
лежит между нулем и единицей. Как указывалось выше, многослойные нейронные
сети обладают большей представляющей мощностью,
чем однослойные, лишь в случае присутствия нелинейности. Сжимающая
функция обеспечивает требуемую нелинейность.