Обобщения и применения модели Хопфилда
Модификации правила Хэбба
Ограничения емкости синаптической памяти, а также проблема ложной памяти классической нейронной сети в модели Хопфилда, обученной по правилу Хебба, привели к появлению целого ряда исследований, целью которых было снятие этих ограничений. При этом главный упор делался на модификацию правил обучения.
Матрица Хебба с ортогонализацией образов
На предыдущей лекции было установлено, что ортогональность
образов обучающей выборки является весьма благоприятным
обстоятельством, так как в этом случае можно показать их устойчивое
сохранение в памяти. При точной ортогональности достигается
максимальная емкость памяти, равная  — максимально возможному
числу ортогональных образов из
— максимально возможному
числу ортогональных образов из  компонент.
компонент.
На этом свойстве ортогональных образов и основан один из наиболее часто используемых способов улучшения правила Хебба: перед запоминанием в нейронной сети исходные образы следует ортогонализовать. Процедура ортогонализации приводит к новому виду матрицы памяти:
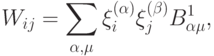
где 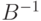 — матрица, обратная к матрице
— матрица, обратная к матрице  :
:
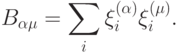
Такая форма матрицы памяти обеспечивает воспроизведение любого
набора из 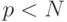 образов. Однако существенным недостатком этого
метода
является его нелокальность: обучение связи между двумя нейронами
требует знания состояний всех других нейронов. Кроме того, прежде чем
начать обучение, необходимо заранее знать все обучающие образы.
Добавление нового образа требует полного переобучения сети. Поэтому
данный подход весьма далек от исходных биологических оснований сети
Хопфилда —Хебба, хотя на практике приводит к заметным улучшениям ее
функционирования.
образов. Однако существенным недостатком этого
метода
является его нелокальность: обучение связи между двумя нейронами
требует знания состояний всех других нейронов. Кроме того, прежде чем
начать обучение, необходимо заранее знать все обучающие образы.
Добавление нового образа требует полного переобучения сети. Поэтому
данный подход весьма далек от исходных биологических оснований сети
Хопфилда —Хебба, хотя на практике приводит к заметным улучшениям ее
функционирования.
Отказ от симметрии синапсов
Другим подходом для улучшения правила Хебба является отказ от симметрии синаптических соединений. Матрица памяти может выбираться в следующей форме:
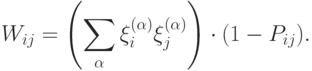
Элементы матрицы 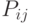 из множества
из множества 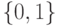 управляют
наличием или отсутствием связи от нейрона
управляют
наличием или отсутствием связи от нейрона  к нейрону
к нейрону 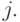
Увеличение емкости памяти в этой модели в принципе может быть
достигнуто за счет появления новых степеней свободы, связанных с
матрицей 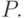 В общем случае, однако, трудно предложить алгоритм
выбора
этой матрицы. Следует также отметить, что динамическая система с
несимметричной матрицей не обязана быть устойчивой.
В общем случае, однако, трудно предложить алгоритм
выбора
этой матрицы. Следует также отметить, что динамическая система с
несимметричной матрицей не обязана быть устойчивой.
