Двоичные числа и двоичная арифметика
Двоичная арифметика
Правила двоичной арифметики
Двоичное сложение
В простейшем случае, для одноразрядных чисел, правила двоичного сложения имеют вид:
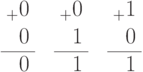
При сложении (  ) возникает два случая:
) возникает два случая:
- когда входной перенос равен
 , получаем
, получаем 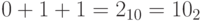 :
: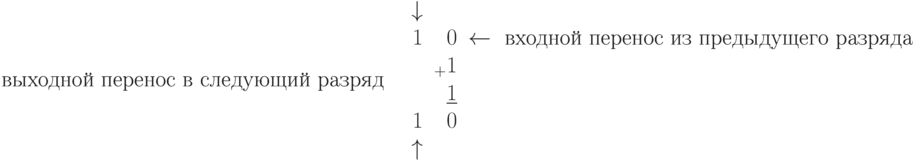
- когда входной перенос равен
 , получаем
, получаем 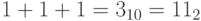 :
:
Многоразрядные числа складываются по тем же правилам, но при этом учитывается входной перенос в каждом разряде: выходной перенос младшего разряда является входным переносом для соседнего старшего разряда. Рассмотрим несколько примеров сложения многоразрядных чисел.
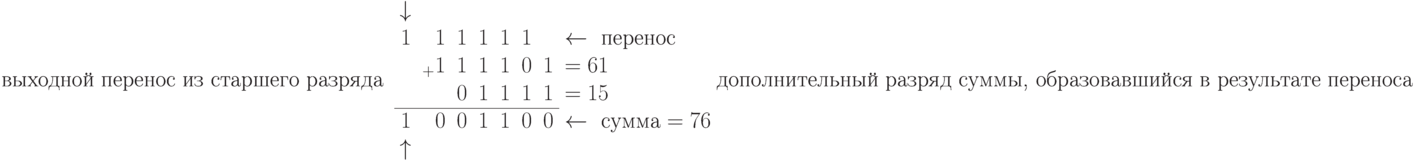
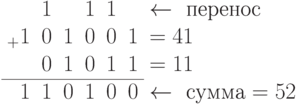
Двоичное вычитание
Здесь рассматриваются правила, работающие в случае вычитания меньшего числа из большего. Все остальные случаи рассматриваются ниже в разделе 3.2, посвященном двоичной арифметике со знаками. В простейшем случае, для каждого разряда, правила двоичного вычитания имеют вид:
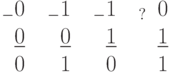
Когда производится вычитание ( 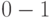 ) осуществляется займ из более старшего разряда. Знак вопроса означает, что разряд уменьшаемого изменяется в результате займа по правилу:
) осуществляется займ из более старшего разряда. Знак вопроса означает, что разряд уменьшаемого изменяется в результате займа по правилу:
При вычитании (0 - 1) в разряде разности получается 1, разряды уменьшаемого, начиная со следующего, изменяются на противоположные (инвертируются) до первой встречной единицы (включительно). После этого производится вычитание из измененных разрядов уменьшаемого.
Рассмотрим несколько примеров вычитания многоразрядных чисел (из большего числа вычитается меньшее).
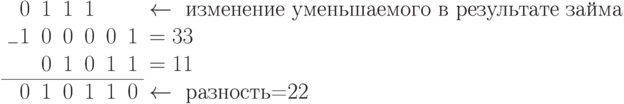
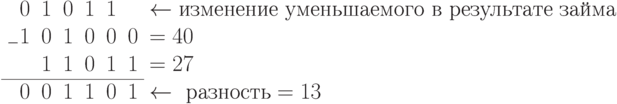
Очевидно, что как в десятичном, так и в двоичном коде, складывать значительно проще, чем вычитать. Поэтому большое распространение получила двоичная арифметика с учетом знаков чисел, где вычитание заменяется сложением чисел с учетом их знака. При этом уже не имеет значения соотношение чисел между собой, какое из них больше - вычитаемое или уменьшаемое. Знак разности получается автоматически.
Двоичная арифметика с учетом знаков чисел
Прямой, обратный и дополнительный коды
В двоичном коде знак числа представляет собой разряд, приписываемый слева от значащих разрядов числа. Знак " 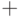 " обозначается логическим
" обозначается логическим  , знак "
, знак "  " - логической
" - логической  . Для наглядности все примеры будем рассматривать для целых чисел, отделяя знаковый разряд точкой.
. Для наглядности все примеры будем рассматривать для целых чисел, отделяя знаковый разряд точкой.
Прямой код (ПК) и для отрицательных, и для положительных чисел образуется одинаково, простым дописыванием знакового разряда.
Так, в восьмиразрядном формате
Обратный код (ОК) для положительных чисел совпадает с прямым, т.е. к значащим разрядам приписывается знаковый разряд. Для отрицательных чисел значащие разряды инвертируются (нули заменяются на единицы, единицы - на нули), после чего приписывается знак.
Для того же числа обратный код имеет вид: 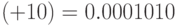 ,
, 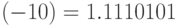 .
.
Недостатком обратного кода является то, что одно и то же число 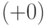 и
и  записывается по-разному:
записывается по-разному: 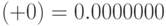 ,
, 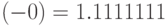 , что может вызвать нежелательное разночтение работы логической схемы. Поэтому предпочтительным является дополнительный код.
, что может вызвать нежелательное разночтение работы логической схемы. Поэтому предпочтительным является дополнительный код.
Дополнительный код (ДК) для положительных чисел совпадает с обратным и прямым, т.е. к значащим разрядам приписывается знаковый разряд. Для отрицательных чисел дополнительный код на 1 больше, чем обратный. После образования значащих разрядов приписывается знаковый разряд.
Для значащих разрядов отрицательного числа справедлива формула:
 |
( 11.3) |
Напишем число  в 7-разрядном дополнительном коде:
в 7-разрядном дополнительном коде:

Таким образом в дополнительном коде 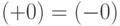 , следовательно, указанный недостаток обратного кода преодолен.
, следовательно, указанный недостаток обратного кода преодолен.
Рассмотрим образование дополнительного кода для числа 10. Для положительного числа 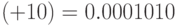 , а для отрицательного числа
, а для отрицательного числа  дополнительный ко д получается следующим образом:
дополнительный ко д получается следующим образом:
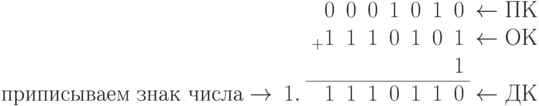
Для замены вычитания сложением применяется и обратный, и дополнительный коды, при этом в каждом из них действуют свои правила.
Двоичная арифметика в дополнительном коде
При решении во избежание типовых ошибок рекомендуется придерживаться следующей последовательности действий. Допустим, заданы два десятичных числа, тогда необходимо:
- перевести десятичные числа в двоичный код;
- уравнять форматы полученных двоичных чисел;
- если знаки чисел одинаковые, добавить по одному резервному нулю слева от каждого числа во избежание переполнения;
- получить дополнительные коды чисел;
- приписать знаковые разряды;
- сложить полученные коды по правилам двоичного сложения;
- перенос из знакового разряда (если он есть) отбросить;
- результат получен в дополнительном коде, поэтому для проверки значащих разрядов отрицательного числа необходимо сделать вычисления, противоположные формуле (11.3): сначала вычислить обратный код по формуле
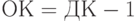 , после чего произвести инверсию полученного числа.
, после чего произвести инверсию полученного числа.
Для наглядности возьмем два десятичных числа, например, 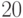 и
и  , и сделаем все возможные варианты вычислений:
, и сделаем все возможные варианты вычислений:
-
 .
.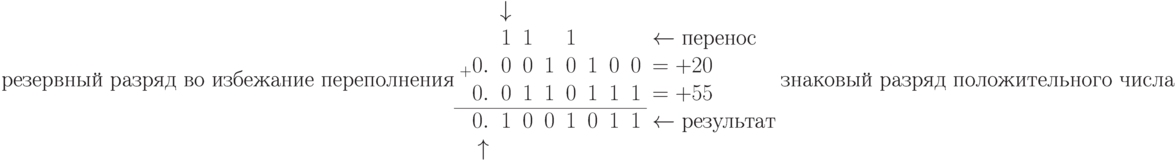
Число положительное, поэтому ОК=ПК, для проверки числа нужно перевести его значащие разряды в десятичный код по (П3-2):
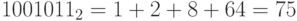 .
. -
 . Сначала получим дополнительный код отрицательного числа
. Сначала получим дополнительный код отрицательного числа  :
: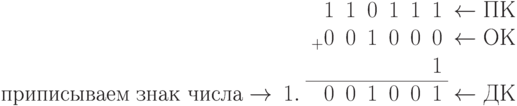
Здесь важно уяснить, что крайние левые нули в значащих разрядах сокращать нельзя, поскольку они являются значимыми. Иными словами, все вычисления для каждого примера производятся в неизменном формате, в данном случае в примере (б) - это шесть значащих разрядов, т.е. столько, сколько содержится в большем числе.
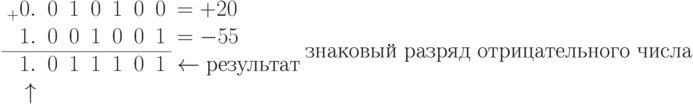
Вновь получили знак числа и его значащие разряды, занимающие жестко заданные позиции в выбранном формате числа. Поскольку получено отрицательное число, то ДК ПК, для проверки его значащих разрядов нужно сначала вычислить обратный код, затем перевести его в прямой код инверсией -
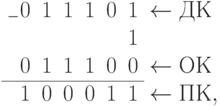
а затем уже перевести его в десятичный код по (П3-2):
 .
. -
 - Сначала получим ДК отрицательного числа
- Сначала получим ДК отрицательного числа  .
.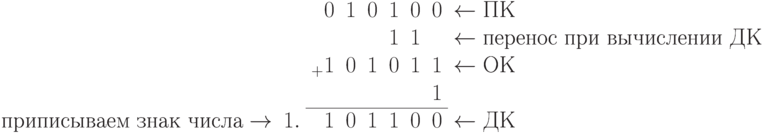
После этого произведем вычисления:
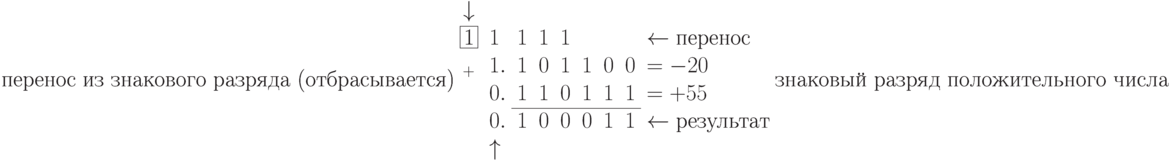
Получено положительное число, поэтому
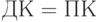 , для проверки результата нужно только перевести значащие разряды в десятичный код:
, для проверки результата нужно только перевести значащие разряды в десятичный код:  .
. -
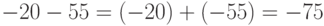 - Сначала получим дополнительный код отрицательных чисел. Для числа
- Сначала получим дополнительный код отрицательных чисел. Для числа  он получается следующим образом:
он получается следующим образом:
А для числа
 -
-
Сложим полученные числа в том же формате:

Поскольку число отрицательное,
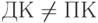 . Для проверки значащих разрядов числа нужно сначала вычислить обратный код, после чего перевести его в прямой код инверсией -
. Для проверки значащих разрядов числа нужно сначала вычислить обратный код, после чего перевести его в прямой код инверсией -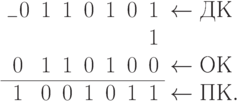
И только после этого полученное число проверяется переводом в десятичный код по (11.2):
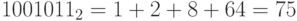 .
.

