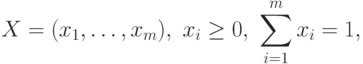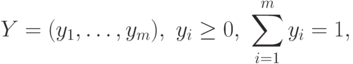Опубликован: 18.05.2011 | Доступ: свободный | Студентов: 978 / 107 | Оценка: 4.40 / 4.20 | Длительность: 12:30:00
Тема: Программирование
Специальности: Программист, Архитектор программного обеспечения
Лекция 23:
Вычислительные эксперименты в моделировании волн-убийц
Лабораторная работа "Матричные игры"
Цель занятия
Провести вычислительные эксперименты с матричными играми с целью исследования оптимальности смешанных стратегий.
Сценарий лабораторной работы
- Написать программу для моделирования матричных игр в интерактивном режиме для двух лиц.
- Задать различные матричные игры, имеющие оптимальные смешанные стратегии.
- Рассчитать для этих матричных игр оптимальные смешанные стратегии.
- Разыграть серию игр с реальными участниками.
- Проанализировать эффективность использования оптимальных смешанных стратегий.
Указания
Игры двух игроков с нулевой суммой удобно записывать в матричном
виде. Пусть множество стратегий первого игрока равно 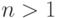 , а
второго -
, а
второго -  , тогда запишем в виде матрицы значения функции выигрышей
, тогда запишем в виде матрицы значения функции выигрышей
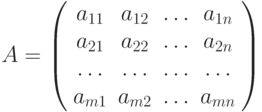
Смешанной стратегией называется случайная величина, значениями которой являются стратегии игрока. Смешанная стратегия - это распределение вероятностей на множестве допустимых стратегий, которую можно представить вектором с неотрицательными компонентами, сумма которых равна единице.
При смешанном расширении понятия матричной игры, игроки выбирают свои смешанные стратегии: первый игрок