Объектно-ориентированный подход к реализации линейных операторов
Цель лекции: Показать как работать с неограниченными линейными операторами в бесконечномерных пространствах.
В функциональном анализе большое значения играют линейные
операторы. Пусть  и
и 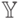 - линейные пространства,
- линейные пространства, 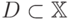 - линейное подпространство. Линейным
оператором
- линейное подпространство. Линейным
оператором 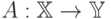 называется такое отображение, что для
любых
называется такое отображение, что для
любых  и
и 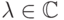 верно
верно
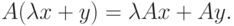
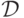 называется областью определения оператора
называется областью определения оператора  , и мы
часто будем обозначать
, и мы
часто будем обозначать 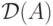 .
.Если пространства  и
и 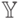 банаховы пространства, то можно
рассматривать непрерывные операторы. Оператор
банаховы пространства, то можно
рассматривать непрерывные операторы. Оператор  называется
непрерывным, если
называется
непрерывным, если 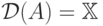 и для любой сходящейся в
и для любой сходящейся в  последовательности
последовательности 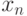 имеет место
имеет место
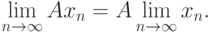
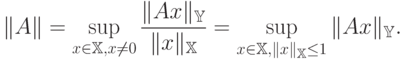
В конечномерном случае, когда 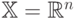 ,
, 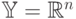 линейные
операторы являются матрицами
линейные
операторы являются матрицами  . Примером неограниченного
оператора является оператор дифференцирования. Пусть
. Примером неограниченного
оператора является оператор дифференцирования. Пусть ![\Bbb{X}=\Bbb{Y}=C[a,b]](/sites/default/files/tex_cache/78dbd20f75ed2eabdfa0ad785358e722.png) , множество
, множество  состоит из непрерывных на
состоит из непрерывных на ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) функций, имеющих непрерывную производную, тогда оператор
функций, имеющих непрерывную производную, тогда оператор
![A[f]=\frac{df}{dx}](/sites/default/files/tex_cache/088fef8a8eeac52962653cd35ed8ba6e.png)
Мы будем рассматривать линейные операторы в бесконечномерных
гильбертовых пространствах. Пусть  - такое гильбертово
пространство, что существует бесконечная последовательность
линейно независимых элементов
- такое гильбертово
пространство, что существует бесконечная последовательность
линейно независимых элементов 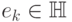 таких, что
таких, что
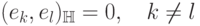

 однозначно представляется рядом
однозначно представляется рядом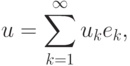
 . Элементы
. Элементы  называются ортонормированным базисом, а сам ряд - абстрактными рядом Фурье. Числа
называются ортонормированным базисом, а сам ряд - абстрактными рядом Фурье. Числа 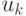 называются коэффициентами
Фурье, и для них имеет место следующая формула
называются коэффициентами
Фурье, и для них имеет место следующая формула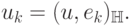
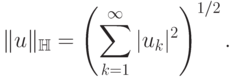
Таким образом, чтобы задать любой элемент пространства  достаточно задать последовательность коэффициентов Фурье, т.е.
таких чисел, что
достаточно задать последовательность коэффициентов Фурье, т.е.
таких чисел, что

Иногда удобно рассматривать ряды, где 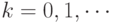 или
или 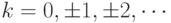 . Для этих случаев все аналогично.
. Для этих случаев все аналогично.
Любой оператор в гильбертовом пространстве можно задать как преобразование последовательности коэффициентов Фурье. Для линейного оператора это преобразование должно быть линейным.
Большой интерес представляют такие линейные операторы, которые
можно представить последовательностью чисел (вообще говоря,
комплексных)  , а действие этого оператора на элемент
следующим образом. Для любого
, а действие этого оператора на элемент
следующим образом. Для любого
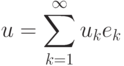
![A[u]=\sum\limits_{k=1}^\infty \alpha_ku_ke_k.](/sites/default/files/tex_cache/9acb15e46493f36a8ee3c59600a730b1.png)
 , то такой оператор будет
ограниченным (и непрерывным). Такие операторы мы будем называть диагональными.
, то такой оператор будет
ограниченным (и непрерывным). Такие операторы мы будем называть диагональными.Классическим примером гильбертова пространства является
пространство 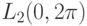 - измеримых на
- измеримых на ![[0,2\pi]](/sites/default/files/tex_cache/1cc5fb6d3b10cf0b4029e23d46fa7fc0.png) функций и
имеющих интегрируемый по Лебегу квадрат модуля на
функций и
имеющих интегрируемый по Лебегу квадрат модуля на ![[0,2\pi]](/sites/default/files/tex_cache/1cc5fb6d3b10cf0b4029e23d46fa7fc0.png) .
Скалярное произведение задается формулой
.
Скалярное произведение задается формулой
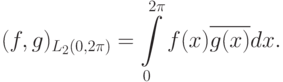
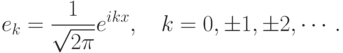
 , тогда этот оператор будет
оператором дифференцирования. Как мы видим, этот оператор не будет
ограниченным и будет определен не на всех функциях, а только на
тех функциях, на которых будет сходится ряд
, тогда этот оператор будет
оператором дифференцирования. Как мы видим, этот оператор не будет
ограниченным и будет определен не на всех функциях, а только на
тех функциях, на которых будет сходится ряд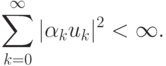
Обратимся к вопросу об объектно-ориентированнной реализации элементов гильбертовых пространств и линейных диагональных операторов.

 предназначен для описания коэффициентов Фурье элементов
гильбертовых пространств, а второй класс
предназначен для описания коэффициентов Фурье элементов
гильбертовых пространств, а второй класс  описывает
диагональный оператор.
описывает
диагональный оператор.Рассмотрим пространство  в котором выберем следующий
базис
в котором выберем следующий
базис
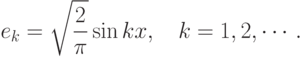
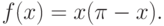

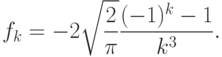
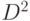 со
следующими числами
со
следующими числами 

![D^2[f]](/sites/default/files/tex_cache/de611e15461e8afa0f712a039ad5ad39.png) нам даже не потребуется компьютер, можно
сразу записать
нам даже не потребуется компьютер, можно
сразу записать=\sum\limits_{k=1}^\infty
\frac{4}{\pi}\frac{(-1)^{k+1}-1}{k}\sin kx.](/sites/default/files/tex_cache/faee2df5f627d6cd72474d344e2d50da.png)
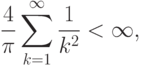
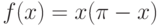 принадлежит
области определения оператора
принадлежит
области определения оператора 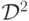 . А теперь заметим, что
разложение функции
. А теперь заметим, что
разложение функции 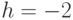 по нашему базису имеет вид
по нашему базису имеет вид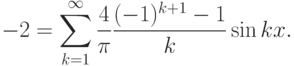
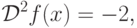
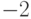 является второй производной по переменной
является второй производной по переменной  от
функции
от
функции  . И это не совпадение - наш оператор
. И это не совпадение - наш оператор 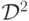 ,
действительно, является оператором дважды дифференцирования. В
этом несложно убедиться, если заметить, что
,
действительно, является оператором дважды дифференцирования. В
этом несложно убедиться, если заметить, что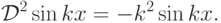
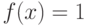 имеет разложение по базису в нашем пространстве
имеет разложение по базису в нашем пространстве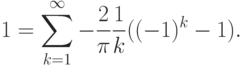
![D^2[1]](/sites/default/files/tex_cache/bad8abdc8b487e997ef6df8fd6ce3152.png) имеют вид
имеют вид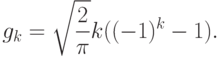
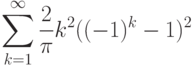
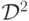 накладывает условия не только на гладкость, но и на краевые
условия - необходимо, чтобы функция принимала нулевые значения
при
накладывает условия не только на гладкость, но и на краевые
условия - необходимо, чтобы функция принимала нулевые значения
при 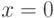 и
и 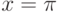 .
.Проверим наши теоретические выкладки с помощью компьютерного моделирования на C#. Для этого мы реализуем следующие классы.
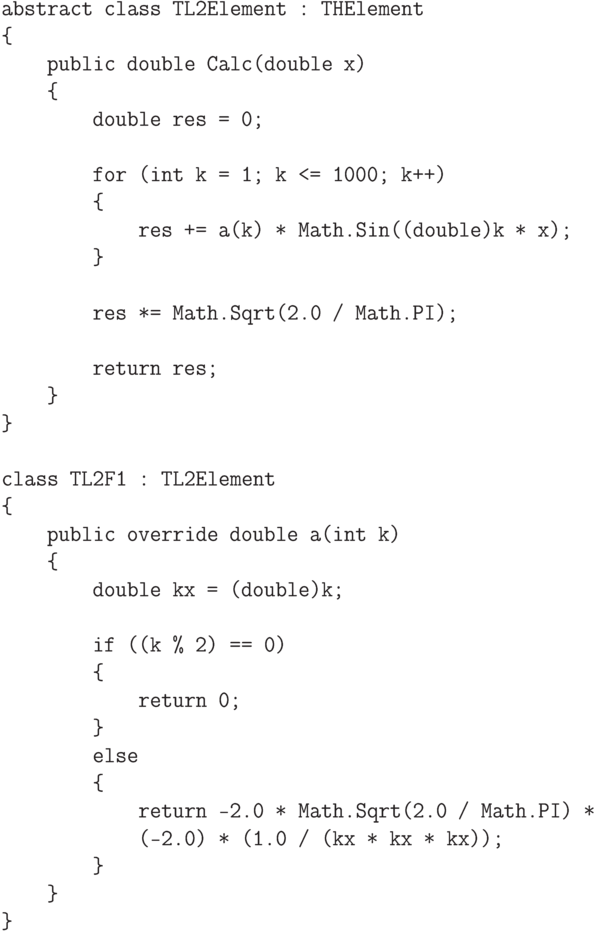
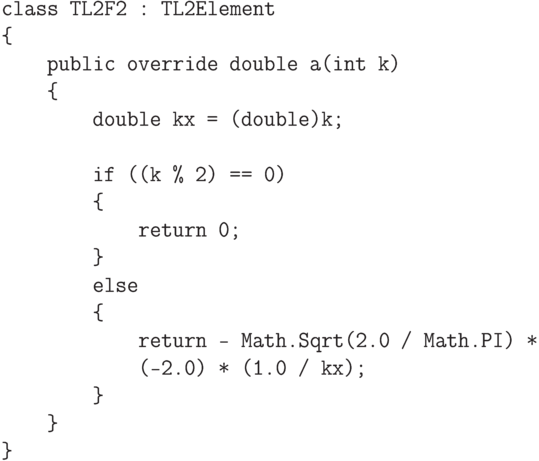
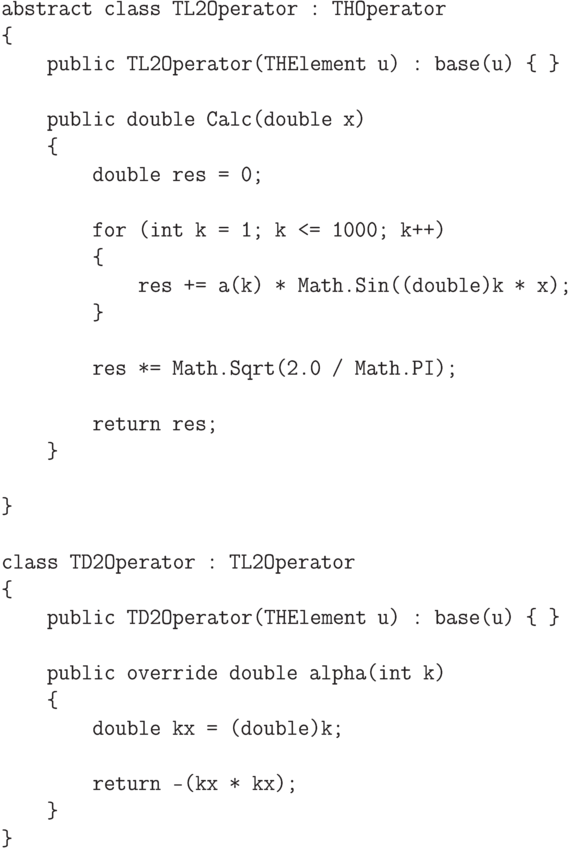
 = {0}", D2.Calc(1.0));
D2 = new TD2Operator(F2);
Console.WriteLine("D2[1](1) = {0}", D2.Calc(1.0));
\end{verbatim}](/sites/default/files/tex_cache/811ac3e3f596dca54e7bbddadc959a76.png)
 = -1.99914825586894
D2[1](1) = 425.069483543905
\end{verbatim}](/sites/default/files/tex_cache/7bdd4dafad328a47a99b68b7091aa9a5.png)
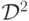 к
функции
к
функции 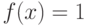 нельзя.
нельзя.Ключевые термины
Абстрактный ряд Фурье - аналог ряда Фурье в гильбертовом пространстве.
Диагональный оператор - оператор, который можно задать путем умножения коэффициентов абстрактного ряда Фурье на числа.
Линейный оператор - линейное отображение одного линейного пространства в другое.
Непрерывный оператор - непрерывное отображение одного метрического пространства в другое.
Краткие итоги: Приведена конструкционная реализация линейных неограниченных операторов в гильбертовом пространстве. Реализованы классы операторов, для представления линейных операторов на языке C#.
