Общие динамические системы
Цель лекции: Показать эффективность объктно-ориентированного подхода для моделирования динамических систем. Создать классы на языке C# для моделирования динамических систем с непрерывным и дискретным временем.
Динамической системой называют математическую модель системы, процессы в которой развиваются во времени. Состояние динамической системы характеризуется фазовыми координатами, которые принадлежат фазовому пространству. Время в динамической системе может быть как непрерывным, так и дискретным. Фазовое множество может быть конечным или бесконечным.
Пусть дано непустое множество 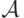 , которое мы будем называть
фазовым пространством, а каждый элемент этого множества
, которое мы будем называть
фазовым пространством, а каждый элемент этого множества 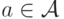 описывает состояние рассматриваемой системы. Через
описывает состояние рассматриваемой системы. Через 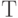 мы будем
обозначать либо множество
мы будем
обозначать либо множество 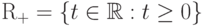 , либо множество
натуральных чисел
, либо множество
натуральных чисел 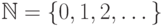 . Это множество будет
играть роль времени. В первом случае мы будем рассматривать
непрерывные динамические системы, а во втором - дискретные.
. Это множество будет
играть роль времени. В первом случае мы будем рассматривать
непрерывные динамические системы, а во втором - дискретные.
Абстрактно заданной динамической системой называется
однопараметрическая полугруппа преобразований множества 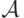
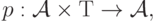
-
 для любого
для любого 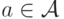 ,
, -
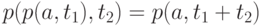 для любых
для любых 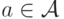 ,
, 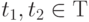 .
.
Соответственно, чтобы задать динамическую систему необходимо
фиксировать множества 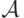 ,
, 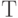 и задать отображение
и задать отображение  ,
удовлетворяющее указанным выше условиям. Пусть
,
удовлетворяющее указанным выше условиям. Пусть 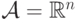 ,
, 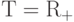 . Рассмотрим систему обыкновенных дифференциальных
уравнений
. Рассмотрим систему обыкновенных дифференциальных
уравнений  -го порядка, которая имеет единственное глобальное
решение для всех
-го порядка, которая имеет единственное глобальное
решение для всех  . Тогда решение этой системы задает
отображение
. Тогда решение этой системы задает
отображение
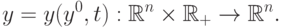
Дискретную динамическую систему можно построить следующим образом.
Пусть у нас некоторое множество 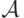 и задан оператор
и задан оператор
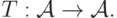
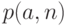 следующим образом
следующим образом
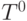 есть единичное отображение. Таким образом мы имеем
дискретную динамическую систему. Содержательные примеры конечной
дискретной динамической системы строятся на основании конечных
автоматов.
есть единичное отображение. Таким образом мы имеем
дискретную динамическую систему. Содержательные примеры конечной
дискретной динамической системы строятся на основании конечных
автоматов.Конечным автоматом называется набор 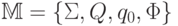 , где
, где  - конечное множество
(входной/выходной алфавит),
- конечное множество
(входной/выходной алфавит),  - конечное множество (внутренние состояния),
- конечное множество (внутренние состояния), 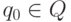 -
начальное состояние,
-
начальное состояние,  - функция переходов
- функция переходов
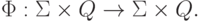
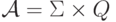 ,
, 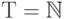 . Будем
обозначать
. Будем
обозначать 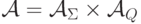 . Отображение
. Отображение  задается по
правилу:
задается по
правилу:
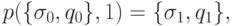
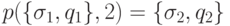
Приступим к реализации класса на C# для описания абстрактной динамической системы.



