НОУ ИНТУИТ | Современные численные методы в объектно-ориентированном изложении на C#. Лекция 17: Обыкновенные дифференциальные уравнения

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 18.05.2011 | Доступ: свободный | Студентов: 978 / 107 | Оценка: 4.40 / 4.20 | Длительность: 12:30:00

Тема: Программирование

Специальности: Программист, Архитектор программного обеспечения

|

Вам нравится? Нравится 18 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Рассматриваются вопросы, связанные с приближенным решением задачи Коши для дифференциальных уравнений. Рассмотрены численные методы решения задачи Коши для дифференциальных уравнений: метод Эйлера и метод Рунге-Кутта. Эти методы реализованы на основе объектно-ориентированного подхода и проведены сравнительные эксперименты.

Ключевые слова: отрезок, функция, обыкновенное дифференциальное уравнение, место, параметр, производные, разрешимость, задача Коши, очередь, методы Рунге-Кутты, точность, метод Эйлера, представление, класс, график, дифференциальное уравнение, приращение функции

Цель лекции: Показать эффективность объектно-ориентированного подхода к задаче нахождения численных решений задачи Коши для дифференциальных уравнений. Провести вычислительные эксперименты и сравнить различные методы.

В настоящей лекции мы будем рассматривать задачу Коши для довольного широкого класса обыкновенных дифференциальных уравнений.

Сначала перейдем к формальному определению постановки задачи Коши. Пусть $D\subset\Bbb{R}^n$ - область (ограниченная или нет) в -мерном пространстве. Пусть также задан отрезок $[0,\Bbb{T}]$ , здесь $\Bbb{T}>0$ может быть и бесконечностью. Введем обозначение

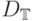$D_\Bbb{T}=\{(x,t):x\in\overline D,t\in[0,\Bbb{T}]\}.$

Пусть в $D_\Bbb{T}$ задана функция f(x,t)

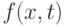тогда можно рассматривать обыкновенное дифференциальное уравнение

$y'(t)=f(y(t),t),\ t\in[0,\Bbb{T}].$

( 16.1)

С этим уравнением связывается начальное условие

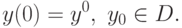$y(0)=y^0,\ y_0\in D.$

( 16.2)

Задача нахождения функции y(t)

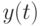такой, что на некотором интервале [0,T]

функция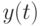

имеет непрерывную производную при $t\in[0,T]$ имеет место $y(t)\in\overline{D}$ , и функция y(t)

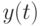удовлетворяет уравнению 16.1 и начальному условию 16.2.

В теории обыкновенных дифференциальных уравнений доказываются следующие теоремы.

Теорема 16.1. Пусть функция 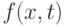f(x,t) является непрерывной в 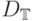$D_\Bbb{T}$ , тогда существует такое T>0 , что на [0,T] существует по крайней мере одно решение задачи 16.1-16.2.

В условиях теоремы существуют примеры задач Коши, которые имеют более одного решения. Действительно, если взять 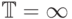$D=\Bbb{R}$ , $\Bbb{T}=\infty$ , а в качестве функции

$f(x,t)=\sqrt{x},$

то задачка Коши

$y'(t)=\sqrt{y(t)},$

имеет бесконечное число решений:

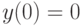
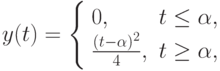
$y(t)=\left\{% \begin{array}{ll} 0, & t\le\alpha, \\ \frac{(t-\alpha)^2}{4}, & t\ge\alpha, \\ \end{array}% \right.$

где $\alpha\ge0$ - параметр семейства решений.

Чтобы гарантировать единственность решения задачи Коши, необходимо накладывать большие условия на функцию .

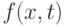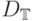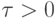Теорема 16.2. Пусть функция f(x,t) является непрерывной в $D_\Bbb{T}$ , и существует такая положительная константа L>0 , зависящая только от $\tau>0$ что для любого отрезка $[0,\tau]\subset[0,\Bbb{T}]$ выполнено неравенство

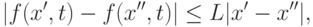$|f(x',t)-f(x'',t)|\le L|x'-x''|,$

( 16.3)

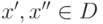для всех $x',x''\in D$ и $t\in[0,\tau]$ .

Тогда существует такое T>0 , что на [0,T] существует единственное решение задачи 16.1-16.2.

Условие 16.3 называется условием Липшица. Это условие будет заведомо выполнено, если непрерывная функция имеет ограниченные и непрерывные производные по в .

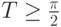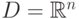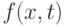Приведенные выше теоремы гарантируют только локальную разрешимость задачи Коши. Действительно, следующий пример задачи Коши не имеет решения на любом отрезке [0,T] , где $T\ge\frac{\pi}{2}$ . Пусть снова $D=\Bbb{R}^n$ , функция f(x,t) имеет вид

тогда задача Коши

имеет единственное решение

$y(t)=\tg t,$

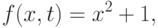
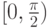которое не продолжается вне интервала $[0,\frac{\pi}{2})$ .

Чтобы гарантировать существование глобального по времени решения, необходимо накладывать дополнительные условия на рост правой части.

Теорема 16.3. Пусть выполнены все условия теоремы 16.2 и дополнительно функция 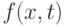f(x,t) удовлетворяет условию в области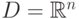 $D=\Bbb{R}^n$

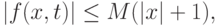
$|f(x,t)|\le M(|x|+1),$

где константа M>0

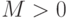не зависит ни от

, ни от

, тогда задача Коши имеет единственное решение на отрезке $[0,\infty)$ .

В курсах по обыкновенным дифференциальным уравнениям проходят разнообразные методы нахождения точных решений дифференциальных уравнений. Однако, во-первых, случаи, когда можно найти точные решения являются исключительными случаями и для многих уравнений доказано, что найти решение в квадратурах невозможно. Во-вторых, даже если удалось найти точное решение, то это решение может быть выражено в неявном виде, либо в виде квадратур, которые в свою очередь могут не выражаться в элементарных случаях. В-третьих, во многих задачах правые части могут не быть заданы элементарными функциями. Наконец, во многих случаях построение приближенного решения с достаточной точностью является значительно более простым и эффективным, чем нахождение точного решения.

Дальше >>

Авторизоваться

Современные численные методы в объектно-ориентированном изложении на C#

Обыкновенные дифференциальные уравнения

Вопросы и ответы