Вычислительные эксперименты в моделировании волн-убийц
Практическое занятие "Матричные игры"
Цель занятия
Провести вычислительные эксперименты с матричными играми с целью исследования оптимальности смешанных стратегий.
Практическая задача
Рассмотрим матричные игры на примере детской игры "камень-ножницы-бумага". Это игра двух игроков с нулевой суммой. Смысл игры состоит в том, что два игрока одновременно выбирают одну из трех стратегий: камень, ножницы или бумага. Один игрок выигрывает у другого если
- он выбрал камень, а противник - ножницы
- он выбрал ножницы, а противник - бумага
- он выбрал бумага, а противник - камень
Если оба игрока выбрали одинаковую стратегию, то фиксируется ничья.
Теперь мы построим математическую модель данной игры. Множество стратегий состоит из трех стратегий
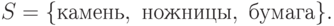
 . Эта матрица будет указывать выигрыш или проигрыш
первого игрока. Будем считать, что при выигрыше противник платит
первому игроку единицу, а при проигрыше первый игрок платит
второму единицу. Вот платежная матрица нашей игры
. Эта матрица будет указывать выигрыш или проигрыш
первого игрока. Будем считать, что при выигрыше противник платит
первому игроку единицу, а при проигрыше первый игрок платит
второму единицу. Вот платежная матрица нашей игры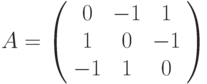
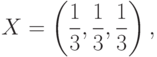
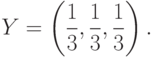
Для проверки проведем вычислительные эксперименты с нашей игрой. Построим класс который с помощью которого мы будем проводить вычислительные эксперименты.
![\begin{verbatim}
class TGame
{
protected double[,] A;
protected int m = 0, n = 0;
Random rnd;
public TGame()
{
rnd = new Random();
}
public double Calc(double[] X, double[] Y, int Count)
{
double res = 0;
int i, j;
for (int k = 0; k < Count; k++)
{
i = Release(X, m);
j = Release(Y, n);
res += GetAij(i, j);
}
return res / (double)Count;
}
\end{verbatim}](/sites/default/files/tex_cache/30a3121f8e862355eef1cbe3c49386ad.png)
![\begin{verbatim}
public int Release(double[] Z, int N)
{
double p = rnd.NextDouble();
double a = 0;
for (int i = 1; i <= N; i++)
{
a += Z[i];
if (p <= a)
{
return i;
}
}
return N;
}
public double GetAij(int i, int j)
{
return A[i, j];
}
public double GetC(double[] X, double[] Y)
{
double res = 0;
int i, j;
for (i = 1; i <= m; i++)
{
for (j = 1; j <= n; j++)
{
res += A[i, j] * X[i] * Y[j];
}
}
return res;
}
}
\end{verbatim}](/sites/default/files/tex_cache/1270a2ced27d51fed543fd2b9ebb001a.png)
![\begin{verbatim}
class TGame3 : TGame
{
public TGame3()
: base()
{
m = 3;
n = 3;
A = new double[4, 4];
A[1, 1] = 0;
A[1, 2] = -1;
A[1, 3] = 1;
A[2, 1] = 1;
A[2, 2] = 0;
A[2, 3] = -1;
A[3, 1] = -1;
A[3, 2] = 1;
A[3, 3] = 0;
}
}
\end{verbatim}](/sites/default/files/tex_cache/68fe3e5d225885acb6b94ca0975c1bb7.png)
Запускать нашу игру будем следующим образом.
![\begin{verbatim}
double[] X;
double[] Y;
double l3 = 1 / 3;
TGame3 Game3 = new TGame3();
X = new double[4] { 0, l3, l3, l3 };
Y = new double[4] { 0, l3, l3, l3 };
Console.WriteLine("Res = {0}", Game3.Calc(X, Y, 1000000));
\end{verbatim}](/sites/default/files/tex_cache/436ba901a4412bb483d996fabfdf6f93.png)
В данном случае мы используем оптимальные смешанные стратегии для
обоих игроков. Вот результат рассчитанной цены игры и результат
розыгрыша 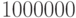 игр.
игр.