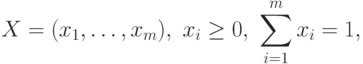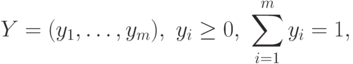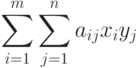Объектно-ориентированный подход к теории игр
Цель лекции: Рассмотреть объектно-ориентированое моделирование матричных игр. Реализовать проверку смешанных стратегий с помощью вычислительных экспериментов.
На прошлой лекции мы рассматривали игру в "крестики-нолики", в которой принимали участие два различных агента. В настоящей лекции мы рассмотрим элементы теории игр. Теория игр - это прикладная математическая дисциплина, в которой изучаются методы нахождения оптимальных решений в условиях неопределенности и ситуациях противодействия со стороны других игроков. Современную математическую форму теория игр приобрела после известного труда Дж. фон Неймана и О. Моргенштерна "Теория игр и экономическое поведение", вышедшего в 1944 году. В настоящее время теория игр находит свое применение в экономических науках, в социальных науках, биологии, а также и в математических дисциплинах, таких как, математическая статистика, функциональный анализ и других.
В отличии от задач оптимизации, где необходимо найти оптимальное решение в заданных условиях, в теории игр необходимо найти оптимальное решение в условиях противодействия со стороны других игроков.
В теории игр рассматривается большое количество постановок различных игр. Мы рассмотрим подробно самую известную постановку в теории игр - антагонистичную игру двух лиц.
Обозначим через  множество всех игроков. Мы будем рассматривать
конечное число игроков. Мы будем различать игроков по номерам
множество всех игроков. Мы будем рассматривать
конечное число игроков. Мы будем различать игроков по номерам
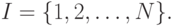
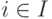 имеет в своем распоряжении
определенное множество стратегий, которое мы обозначим через
имеет в своем распоряжении
определенное множество стратегий, которое мы обозначим через 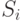 .
.Процедура игры происходит следующим образом: каждый игрок выбирает
одну стратегию из своего множества стратегий 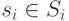 . Вектор
выбранных стратегий всех игроков обозначим через
. Вектор
выбранных стратегий всех игроков обозначим через
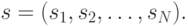
 называется ситуацией в игре. Множество всех
возможных ситуаций можно ввести по формуле
называется ситуацией в игре. Множество всех
возможных ситуаций можно ввести по формуле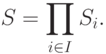
 в
ситуации
в
ситуации  обозначим через
обозначим через 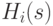 . Функция
. Функция 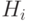 , определенная
на множестве всех ситуаций
, определенная
на множестве всех ситуаций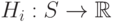
 -го игрока. Мы будем измерять
выигрыши действительными числами, хотя не всегда выигрыш может
быть измерен числом.
-го игрока. Мы будем измерять
выигрыши действительными числами, хотя не всегда выигрыш может
быть измерен числом.Бескоалиционной игрой называется система

 ,
, 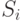 являются множествами, а
являются множествами, а 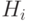 - функции на
множестве
- функции на
множестве  , принимающие вещественные значения.
, принимающие вещественные значения.Наиболее часто встречается ситуация, когда сумма выигрышей всех игроков во всех ситуациях является постоянной, что соответствует тому, что игроки по сути делят между собой фиксированную сумму. Игра называется игрой с постоянной суммой, если
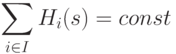
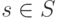 .
.Мы будем рассматривать антагонистичные игры. Игра называется
антагонистичной, если число игроков равно двум, т.е.  ,
а значения функций выигрыша в сумме равны нулю
,
а значения функций выигрыша в сумме равны нулю
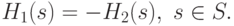
Если в теории оптимизации основной задачей является нахождения
оптимальных решений, то в теории игр аналогом этого является
нахождения ситуации равновесия. Ситуация 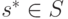 называется ситуацией равновесия в игре, если ни одному из игроков не
выгодно отступать от этой стратегии. формально это можно записать
следующей формулой
называется ситуацией равновесия в игре, если ни одному из игроков не
выгодно отступать от этой стратегии. формально это можно записать
следующей формулой 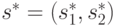

Если множества стратегий конечны, то антагонистичные игры удобно
записывать в матричном виде. Пусть множество стратегий первого
игрока равно 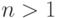 , а второго -
, а второго -  , тогда запишем в виде
матрицы значения функции выигрышей
, тогда запишем в виде
матрицы значения функции выигрышей
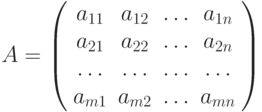
В матричной игре ситуация 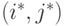 называется равновесной, если
называется равновесной, если
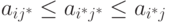
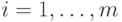 и
и 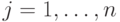 . В теории игр доказывается,
что для существования ситуации равновесия необходимо и достаточно,
чтобы было выполнено равенство
. В теории игр доказывается,
что для существования ситуации равновесия необходимо и достаточно,
чтобы было выполнено равенство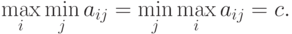
 в этом случае называется ценой игры. Если бы в каждой
игре существовала бы ситуация равновесия, то игры бы не имели
смысл. К счастью или к сожалению, но во многих играх ситуации
равновесия не существует. Самый простой пример - игра в
"чет--нечет". Матрица этой игры такова
в этом случае называется ценой игры. Если бы в каждой
игре существовала бы ситуация равновесия, то игры бы не имели
смысл. К счастью или к сожалению, но во многих играх ситуации
равновесия не существует. Самый простой пример - игра в
"чет--нечет". Матрица этой игры такова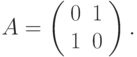
При смешанном расширении понятия матричной игры, игроки выбирают свои смешанные стратегии: первый игрок