Современные численные методы в объектно-ориентированном изложении на C#
[+]
Опубликован: 18.05.2011 | Доступ: свободный | Студентов: 976 / 106 | Оценка: 4.40 / 4.20 | Длительность: 12:30:00
Тема: Программирование
Специальности: Программист, Архитектор программного обеспечения
Теги: objective-c, алгоритмы, анализ, вычисления, графика, динамическая система, дифференциальные уравнения, игры, коэффициенты Фурье, кубический сплайн, матричная игра, машина поста, метод Эйлера, методы рунге-кутты, метрическое пространство, моделирование, программирование, процедуры, теория, трансцендентное уравнение, функциональное пространство, элементы
Лекция 16:

Приближение сплайнами
A
|
версия для печати
< Лекция 15 || Лекция 16: 123 || Лекция 17 >

Практическое занятие "Аппроксимация функций"

Цель занятия

Практическое проведение интерполяции для конкретных функций и изучение свойств интерполяционных функций.

Практическая задача

В настоящем занятии мы разберем пример построения интерполяционного многочлена в форме Лагранжа. Мы рассмотрим простейшую функцию

f(x)=\sin x
Возьмем известные значения этой функции в точках
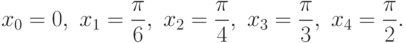
x_0=0,\ x_1=\frac{\pi}{6},\ x_2=\frac{\pi}{4},\ x_3=\frac{\pi}{3},\ x_4=\frac{\pi}{2}.
В этих точках наша функция, как известно, принимает следующие значения
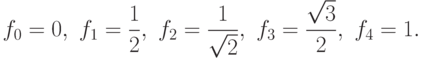
f_0=0,\ f_1=\frac{1}{2},\ f_2=\frac{1}{\sqrt{2}},\ f_3=\frac{\sqrt{3}}{2},\ f_4=1.
Построим интерполяционный многочлен в форме Лагранжа по этим точкам. Согласно известным формулам этот многочлен имеет следующий вид
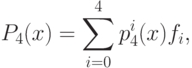
P_4(x)=\sum\limits_{i=0}^4p^i_4(x)f_i,
где
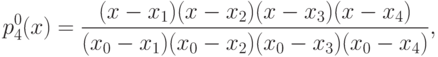
p^0_4(x)=\frac{(x-x_1)(x-x_2)(x-x_3)(x-x_4)} {(x_0-x_1)(x_0-x_2)(x_0-x_3)(x_0-x_4)},
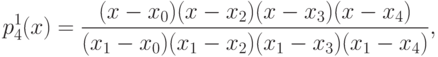
p^1_4(x)=\frac{(x-x_0)(x-x_2)(x-x_3)(x-x_4)} {(x_1-x_0)(x_1-x_2)(x_1-x_3)(x_1-x_4)},
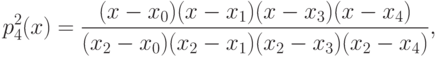
p^2_4(x)=\frac{(x-x_0)(x-x_1)(x-x_3)(x-x_4)} {(x_2-x_0)(x_2-x_1)(x_2-x_3)(x_2-x_4)},
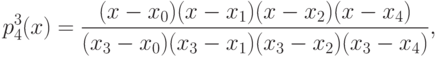
p^3_4(x)=\frac{(x-x_0)(x-x_1)(x-x_2)(x-x_4)} {(x_3-x_0)(x_3-x_1)(x_3-x_2)(x_3-x_4)},
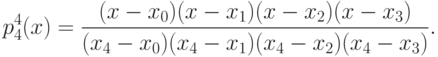
p^4_4(x)=\frac{(x-x_0)(x-x_1)(x-x_2)(x-x_3)} {(x_4-x_0)(x_4-x_1)(x_4-x_2)(x_4-x_3)}.

Для использования этого многочлена, разумеется, нет необходимости раскрывать скобки. Для работы с этим многочленом мы напишем небольшой код на языке C#.

\begin{verbatim} double pi = Math.PI; int N = 4; double[] xn = { 0, pi / 6.0, pi / 4.0, pi / 3.0, pi / 2.0 }; double[] fn = { 0, 1.0 / 2.0, 1.0 / Math.Sqrt(2.0), Math.Sqrt(3.0) / 2.0, 1 }; double[] hn = new double[N + 1]; int i, j; for (i = 0; i <= N; i++) { hn[i] = 1.0; for (j = 0; j <= N; j++) { if (i == j) { continue; } hn[i] *= xn[i] - xn[j]; } } \end{verbatim}
\begin{verbatim} double x = pi / 5.0; double res = 0; for (i = 0; i <= N; i++) { double y; y = fn[i] / hn[i]; for (j = 0; j <= N; j++) { if (i == j) { continue; } y *= (x - xn[j]); } res += y; } Console.WriteLine("sin(pi/5) = {0}; Delta = {1}", res, Math.Abs(res - Math.Sin(x))); \end{verbatim}

В этой программе мы вычисляем значение нашего интерполяционного многочлена в промежуточной точке 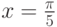x=\frac{\pi}{5} и сравниваем с "точным" значением \sin \frac{\pi}{5}. После запуска мы получим следующий результат.

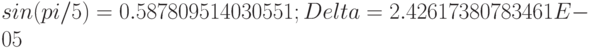
sin(pi/5) = 0.587809514030551; Delta = 2.42617380783461E-05

Можно считать, что это очень не плохой результат для интерполяции функции по столь малому количеству точек.

Дальше >>
< Лекция 15 || Лекция 16: 123 || Лекция 17 >

Вопросы и ответы

вопросов: 0