Линейные уравнения
Цель лекции: Дать математическую постановку вычислительных проблем линейной алгебры. Показать, что известная структура матрицы позволяет строить более эффективные численные методы.
Задачи линейно алгебры относятся основным методам вычислительной математики. Это обусловлено тем, что линейные модели играют первостепенную роль, а их численная реализация требует решать задачи линейной алгебры. В отличии от задач математической физики задачи линейной алгебры являются конечномерными. К основным задачам линейной алгебры можно отнести задачи:
- Решения систем линейных алгебраических уравнений.
- Нахождение обратных матриц, а также приведение матриц к каноническому виду (диагональному или к форме Жордана).
- Нахождение собственных значений и собственных функций матриц.
Мы рассмотрим первую наиболее часто встречающуюся задачу нахождения решений систему линейных алгебраических уравнений с невырожденной квадратной матрицей. Матрица называется невырожденной, если ее определитель не равен нулю.
Будем рассматривать квадратную матрицу
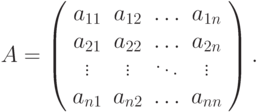
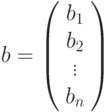
 |
( 12.1) |
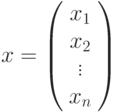
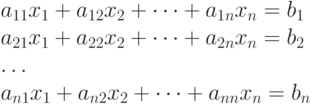
 неособая, т.е.
неособая, т.е. 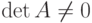 , то задача 12.1 имеет
единственное решение для любой правой части
, то задача 12.1 имеет
единственное решение для любой правой части  . Однако на
практике нахождение решений даже матриц небольшой размерности
может составлять большую проблему. Дело в том, что если
рассмотреть систему
. Однако на
практике нахождение решений даже матриц небольшой размерности
может составлять большую проблему. Дело в том, что если
рассмотреть систему  , то решение этой системы имеет
геометрический смысл точки пересечения двух прямых, заданный
первым и вторым уравнением. Легко себе представить ситуацию, когда
угол пересечения этих прямых может быть очень малым.
, то решение этой системы имеет
геометрический смысл точки пересечения двух прямых, заданный
первым и вторым уравнением. Легко себе представить ситуацию, когда
угол пересечения этих прямых может быть очень малым.Для количественной оценки "сложности" решения задачи существует
понятие числа обусловленности матрицы  . Для неособой
матрицы
. Для неособой
матрицы  число обусловленности вводится по формуле
число обусловленности вводится по формуле
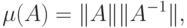
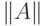 - норма матрицы, которая вводиться для матрицы
- норма матрицы, которая вводиться для матрицы  ,
как для ограниченного линейного оператора в пространстве
,
как для ограниченного линейного оператора в пространстве 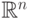 .
Можно показать, что число обусловленности
.
Можно показать, что число обусловленности  всегда превосходит
единицу. Чем больше это число, тем "сложнее" будет решить задачу
нахождение решения этой задачи.
всегда превосходит
единицу. Чем больше это число, тем "сложнее" будет решить задачу
нахождение решения этой задачи.При решении задач нахождения решения системы линейных алгебраических уравнений можно выделить два подхода: точные методы нахождения решений и итерационные методы. Сначала рассмотрим "точные" методы решения системы линейных алгебраических уравнений. Слово "точные" мы пишем в кавычках, поскольку хотя нахождение решения можно осуществить этими методам за конечное число операций, однако среди этих операций обязательно есть операции деления а, как мы уже отмечали, операция деления не всегда может быть реализованы точно.
Главным методом для прямого нахождения решений системы линейных
алгебраических уравнений является метод Гаусса. Этот метод
иногда называют методом исключения неизвестных. Суть этого метода
состоит в том, чтобы сначала из первого уравнения выразить  через коэффициенты матрицы, правую часть и
через коэффициенты матрицы, правую часть и  ,
, 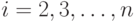 .
Подставив это выражение для
.
Подставив это выражение для  в остальных уравнениях, можно
получить другую систему линейных алгебраических уравнений порядка
в остальных уравнениях, можно
получить другую систему линейных алгебраических уравнений порядка  . Таким образом можно получить одно линейное
уравнение относительно
. Таким образом можно получить одно линейное
уравнение относительно 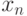 , которое решается тривиально.
Вычислив
, которое решается тривиально.
Вычислив 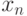 через коэффициенты матрицы
через коэффициенты матрицы  и правую часть
и правую часть  ,
используя полученные ранее выражения для
,
используя полученные ранее выражения для 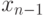 через
через 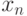 ,
, 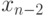 через
через 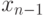 и
и 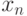 и т.д., можно вычислить все
и т.д., можно вычислить все  ,
, 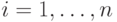 . Условием для выполнения этого метода
является возможность осуществлять выражение
. Условием для выполнения этого метода
является возможность осуществлять выражение  . Если матрица
. Если матрица  является неособой, то условие осуществимости метода Гаусса
всегда выполнено.
является неособой, то условие осуществимости метода Гаусса
всегда выполнено.
Следует отметить, что решение системы линейных алгебраических уравнений с полной матрицей, т.е. когда матрица не имеет специальной структуры заполнения, представляет собой довольно сложную проблему. К счастью, часто в задачах возникают системы уравнений с матрицами специального вида. Для этих случаев существуют отдельные методы, которые могут быть значительно эффективнее метода Гаусса.
Часто возникают уравнения с симметричной положительно определенной
матрицей. Для таких уравнений мы рассмотрим метод Холецкого.
Пусть наша система уравнений задана с помощью симметричной
положительно определенной матрицей  . Метод Холецкого состоит в
том, чтобы представить матрицу
. Метод Холецкого состоит в
том, чтобы представить матрицу  в виде
в виде
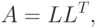
 - нижняя треугольная матрица
- нижняя треугольная матрица 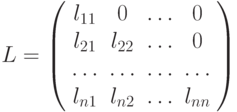 Если мы построим разложение
Если мы построим разложение 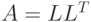 , то уравнение 12.1
может быть заменено двумя уравнениями, которые можно
последовательно решить
, то уравнение 12.1
может быть заменено двумя уравнениями, которые можно
последовательно решить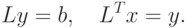
 находятся последовательно по
формулам
находятся последовательно по
формулам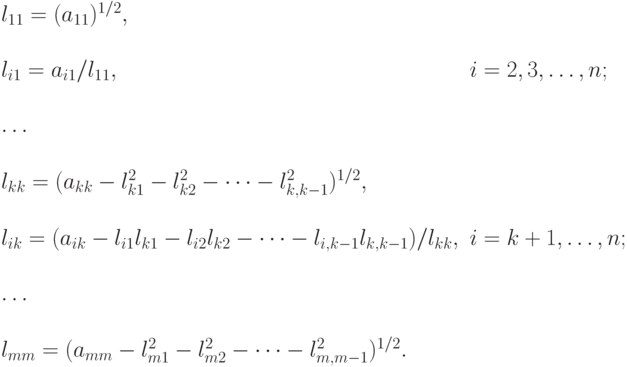
В приложениях часто возникают другие уравнения специального вида. В этих уравнениях матрица является трехдиагональной. Для таких уравнений существует очень эффективный алгоритм, называемый методом прогонки.
Пусть нам необходимо решить следующее уравнение
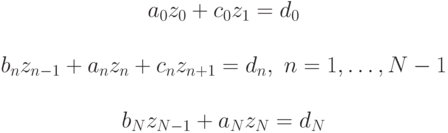 |
( 12.2) |
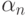 и
и 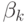 согласно следующим рекуррентным соотношениям
согласно следующим рекуррентным соотношениям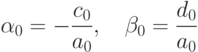
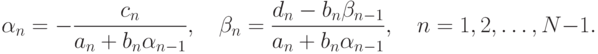
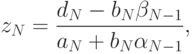
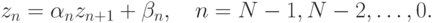
Приведем класс на языке C#, который будем обращать трехдиагональную матрицу методом прогонки.
![\begin{verbatim}
class TProgon
{
public double[] a;
public double[] b;
public double[] c;
public double[] d;
public double[] z;
double[] alpha;
double[] beta;
public void CalcZ()
{
int N = a.Count();
alpha = new double[N];
beta = new double[N];
z = new double[N + 1];
alpha[0] = -c[0] / a[0];
beta[0] = d[0] / a[0];
\end{verbatim}](/sites/default/files/tex_cache/53c003dde7d02be91b254af54ac597d5.png)
![\begin{verbatim}
int n;
for (n = 1; n < N; n++)
{
alpha[n] = -(c[n]) / (a[n] + b[n] * alpha[n - 1]);
beta[n] = (d[n] - b[n] * beta[n - 1]) /
(a[n] + b[n] * alpha[n - 1]);
}
z[N] = (d[N] - b[N] * beta[N - 1]) /
(a[N] + b[N] * alpha[N - 1]);
for (n = N - 1; n <= 0; n--)
{
z[n] = alpha[n] * z[n + 1] + beta[n];
}
}
}
\end{verbatim}](/sites/default/files/tex_cache/c31b2b26515757e33ebe887f3370bf5c.png)
Ключевые термины
Невырожденная матрица - квадратная матрица с определителем отличным от нуля.
Число обусловленности матрицы - числовая характеристика вычислительной сложности обращения матрицы.
Метод Гаусса - основной метод нахождения решений системы линейных алгебраических уравнений с помощью последовательного исключения неизвестных.
Метод Холецкого - метод для обращения симметричных положительно определенных матриц.
Метод прогонки - метод для обращения трехдиагональной матрицы.
Краткие итоги: Рассмотрены численные методы решения задач линейной алгебры. Приведены различные методы, соответствующие матрицам специального вида.
