О решении операторных уравнений

Практическое занятие "Реализация операторов в гильбертовых пространствах"

Цель занятия

Продемонстрировать на характерных примерах реализацию линейных операторов в сепарабельных гильбертовых пространствах.

Практическая задача

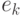Будем рассматривать абстрактное гильбертово пространство , которое задано с помощью своего ортонормированного базиса . Если в качестве пространства взять гильбертово пространство , то в качестве ортонормированного базиса можно взять систему функций

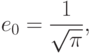
Рассмотрим реализацию линейного оператора, действующего в пространстве , заданного с помощью бесконечной матрицы. Зададим формально бесконечную матрицу как множество

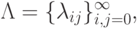
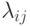где суть комплексные числа, которые убывают по модулю достаточно быстро.

Действие оператора на некоторый элемент

можно вычислить по формуле Мы будем предполагать, что все возникающие у нас ряды являющиеся сходящимися.

На лекциях мы встречались с операторами, которые представлялись диагональной матрицей, и по сути сводились к умножению коэффициентов Фурье на числа. Сейчас мы рассмотрим более общие операторы.

В качестве примера рассмотрим оператор , который задается матрицей

здесь - .

Пусть мы рассматриваем пространство с заданным выше ортонормированным базисом. Рассмотрим функцию 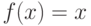. Эта функция представляется следующим рядом Фурье

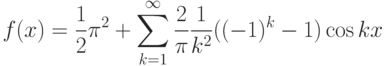
После действия нашим оператором мы получим функцию, которая представляется следующим рядом Фурье

Рассмотрим еще интересный оператор , действие которого можно описать следующим образом. Пусть задан элемент пространства своим рядом Фурье

Тогда элемент будет задаваться следующим рядом Фурье Посмотрим как действует этот оператор в пространстве . Рассмотрим простейшую функцию 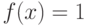. Представим эту функцию в виде ряда Фурье После действия оператора на эту функцию мы получим функцию , представимую в виде

Для оператора можно привести обратный оператор , который действует согласно следующей формуле

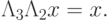
Легко видеть, что для любого элемента имеет место Равенство верно только для таких , для которых 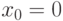.