|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Прикладная теория организации очередей
Пример 13.4.3: Система с программным управлением (см. пример 13.4.1)
Предположим, что компьютерная система в Примере 13.4.1 работает с дисциплиной "приоритетное возвращение к работе". Находим: Тип 1 - самый высокий приоритет:
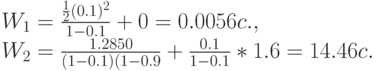
Тип приоритета 2:
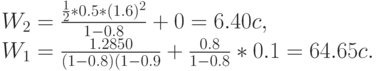
Это показывает что, изменяя состав клиентов типа 1, мы можем обеспечить этим клиентам очень короткое время ожидания, не нарушая характеристик очереди для клиентов типа 2, но обратное преобразование не обеспечивает такого свойства.
Закон сохранения справедлив только для приоритетных систем организации очереди, если приоритетные времена прерывания обслуживания являются экспоненциально распределенными. В общем случае работа может прерываться несколько раз, и поэтому  не будет определять остающееся время обслуживания.
не будет определять остающееся время обслуживания.
M/M/n с приоритетным возвращением к работе
Для 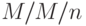 случай приоритетного возвращения к работе анализируется более сложно. Все клиенты должны иметь одинаковое среднее время обслуживания. Сначала среднее время ожидания может быть получено рассмотрением каждого класса автономно (12.15). Затем можно рассмотреть два класса вместе и получить время ожидания для двух классов и т.д. Закон сохранения справедлив, когда все клиенты имеют одинаковое экспоненциально распределенное время обслуживания.
случай приоритетного возвращения к работе анализируется более сложно. Все клиенты должны иметь одинаковое среднее время обслуживания. Сначала среднее время ожидания может быть получено рассмотрением каждого класса автономно (12.15). Затем можно рассмотреть два класса вместе и получить время ожидания для двух классов и т.д. Закон сохранения справедлив, когда все клиенты имеют одинаковое экспоненциально распределенное время обслуживания.
Системы организации очереди с постоянными временами занятия
В этой секции мы сосредотачиваем свое внимание на системе организации очереди 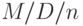 , FCFS. Системы с постоянными временами обслуживания имеют определяющее свойство: клиенты покидают обслуживающие приборы в том же самом порядке, в котором они приняты для обслуживания.
, FCFS. Системы с постоянными временами обслуживания имеют определяющее свойство: клиенты покидают обслуживающие приборы в том же самом порядке, в котором они приняты для обслуживания.
Исторические замечания по M/D/n
Системы организации очереди с Пуассоновским потоком вызовов и постоянными временами обслуживания были проанализированы первыми. Интуитивно можно было бы думать, что анализ более систем с постоянными временами обслуживания проще, чем с экспоненциально распределенными временами обслуживания, но это явно не так. С экспоненциальным распределением иметь дело проще из-за отсутствия у него памяти: остающееся время "жизни" имеет то же самое распределение, как полное время "жизни" (секция 4.1), и поэтому мы можем забыть о периоде или моменте времени, когда начинается время обслуживания. Постоянные времена занятия требуют, чтобы мы помнили точное время начала. Эрланг первым проанализировал систему с постоянным временем обслуживания 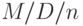 , FCFS (Brockmeyer, 1948 [11] ):
, FCFS (Brockmeyer, 1948 [11] ):
Эрланг: 1909 n = 1 ошибка для n > 1,
Эрланг: 1917 n = 1, 2, 3 без доказательства,
Эрланг: 1920 n - произвольное, решения для n = 1, 2, 3.
Эрланг получил распределение времени ожидания, но не рассматривал вероятности состояния. Фрей (Fry (1928 [30] )) также исследовал 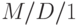 и получил вероятности состояния (уравнения состояния Фрея), используя принцип статистического равновесия Эрланга. Сам Эрланг применял другие теоретические методы.
и получил вероятности состояния (уравнения состояния Фрея), используя принцип статистического равновесия Эрланга. Сам Эрланг применял другие теоретические методы.
Кроммелин (1932 [20] , 1934 [21] ), британский телефонный инженер, представил общее решение для 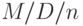 . Он обобщил уравнения состояний Фрея для произвольного
. Он обобщил уравнения состояний Фрея для произвольного  , и получил распределение времени ожидания, теперь называемое распределением Кроммелина.
, и получил распределение времени ожидания, теперь называемое распределением Кроммелина.
Поллячек (1930-34) представил общее, зависимое от времени поступления решение для произвольного распределения времени обслуживания. Согласно предположению о статистическом равновесии он получил явные решения для экспоненциально распределенного и постоянного времен обслуживания.
Хинчин (1932 [63] ) исследовал 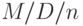 и получил распределение времени ожидания.
и получил распределение времени ожидания.
Вероятности состояния M/D/1
Вероятности состояний для 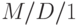 могут быть получены простым способом, исходя из предположения о статистическом равновесии.
могут быть получены простым способом, исходя из предположения о статистическом равновесии.
Пусть интенсивность поступления вызовов равна  , а постоянное время занятия -
, а постоянное время занятия -  . Рассматриваем чистую систему с ожиданием и с единственным обслуживающим прибором.
. Рассматриваем чистую систему с ожиданием и с единственным обслуживающим прибором.
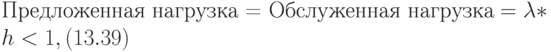 |
( 13.39) |
то есть
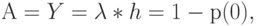
в каждом состоянии, кроме нулевого, обслуженная нагрузка равна 1 Эрл.
Мы рассматриваем два периода (момента времени)  и
и 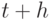 на расстоянии
на расстоянии  . Каждый клиент, обслуживаемый в период
. Каждый клиент, обслуживаемый в период  (самое большее один период), может покинуть обслуживающий прибор в период
(самое большее один период), может покинуть обслуживающий прибор в период 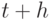 . Клиенты, прибывающие в течение интервала
. Клиенты, прибывающие в течение интервала 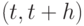 , находятся все еще в очереди в период
, находятся все еще в очереди в период 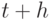 (ожидание или обслуживание).
(ожидание или обслуживание).
Процесс поступления вызовов - Пуассоновский процесс. Следовательно, мы имеем Пуассоновское распределение прибытия во временном интервале 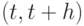 :
:
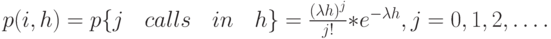 |
( 13.40) |
Вероятность того, что данное состояние в период 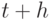 может быть получено из состояния в период
может быть получено из состояния в период  , определяется, принимая во внимание общее количество вызовов и выходы из состояния в течение
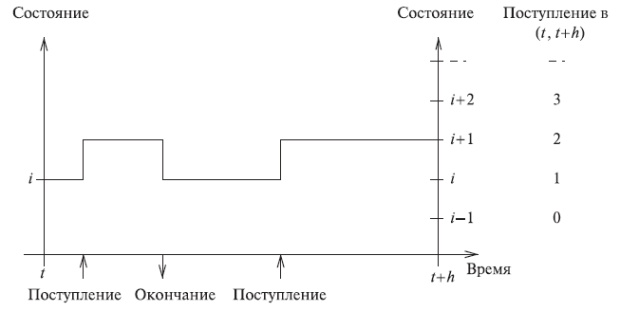
, определяется, принимая во внимание общее количество вызовов и выходы из состояния в течение 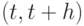 . Рассматривая эти периоды, получаем марковскую цепь, внедренную в первоначальный процесс обслуживания нагрузки (рис.13.4).
. Рассматривая эти периоды, получаем марковскую цепь, внедренную в первоначальный процесс обслуживания нагрузки (рис.13.4).
Мы получаем уравнения состояний Фрея для 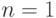 (Fry, 1928 [30] ):
(Fry, 1928 [30] ):
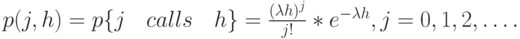 |
( 13.40) |
Выше было установлено:
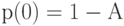
и согласно предположению о статистическом равновесии 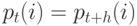 , мы последовательно находим:
, мы последовательно находим:

и далее
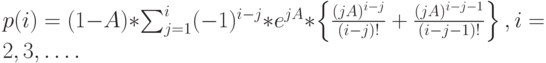 |
( 13.42) |
Последнее слагаемое, соответствующее  , всегда равняется
, всегда равняется 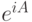 , поскольку
, поскольку 
В принципе  может быть получено из условия, что все вероятности состояния должны в сумме давать единицу.
может быть получено из условия, что все вероятности состояния должны в сумме давать единицу.
Средние времена ожидания и период занятости M/D/1
Для Пуассоновского процесса поступления вызовов вероятность задержки  равна вероятности того, что он не находится в нулевом состоянии (свойство PASTA ):
равна вероятности того, что он не находится в нулевом состоянии (свойство PASTA ):
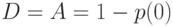 |
( 13.43) |
 обозначает среднее время ожидания для всех клиентов, и w обозначает среднее время ожидания для клиентов, которые стоят в очереди (положительное значение времени ожидания). Мы имеем для любой системы организации очереди (3.20):
обозначает среднее время ожидания для всех клиентов, и w обозначает среднее время ожидания для клиентов, которые стоят в очереди (положительное значение времени ожидания). Мы имеем для любой системы организации очереди (3.20):
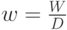 |
( 13.44) |
 и
и  могут быть легко получены, используя формулу Поллячека-Хинчина (13.2):
могут быть легко получены, используя формулу Поллячека-Хинчина (13.2):
 |
( 13.45) |
 |
( 13.46) |
Средняя величина периода занятости была получена для  в (13.7) и иллюстрирована для постоянных времен обслуживания на рис.13.1:
в (13.7) и иллюстрирована для постоянных времен обслуживания на рис.13.1:
 |
( 13.47) |
Среднее время ожидания для задержанных клиентов, таким образом, - половина периода занятости. Это показывает, что вызовы от клиентов прибывают случайно в течение периода занятости, но мы знаем, что ни один вызов не поступает в течение последнего времени обслуживания периода занятости.
Можно показать, что распределение числа вызовов, прибывающих в течение периода занятости, можно выразить распределением Бореля (Borel ):
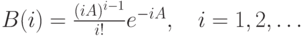 |
( 13.48) |
Распределение времени ожидания: M/D/1, FCFS
Можно показать, что:
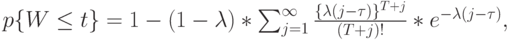 |
( 13.49) |
где 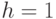 выбрано как единица времени,
выбрано как единица времени, 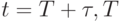 - целое число, и
- целое число, и 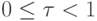 .
.
Граф распределения времени ожидания имеет нарушения каждый раз, когда время ожидания превышает кратное число постоянного времени занятия. Пример для распределения вероятности дополнения времени ожидания  показан на рис.13.5.
показан на рис.13.5.
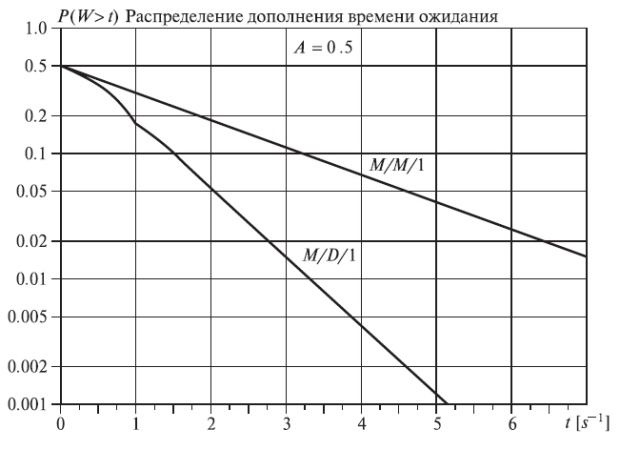
Рис. 13.5. Распределение дополнения времени ожидания для всех клиентов в системе организации очереди M/M/1 и M/D/1 для дисциплины очереди (FCFS). Единица времени = среднее время обслуживания. Заметим, что среднее время ожидания для M/D/1 - только половина времени для M/M/1.
Формула (13.49) неудобна для числовой оценки. Можно показать (Iversen, 1982 [39] ), что формула времени ожидания может быть записана в более компактной форме, например, введенной Эрлангом в 1909 г.:
 |
( 13.50) |
и может применяться для числовой оценки при малых временах ожидания.
Для больших времен ожидания мы обычно интересуемся составными значениями  . Можно показать (Iversen, 1982 [39] ), что для составного значения
. Можно показать (Iversen, 1982 [39] ), что для составного значения 
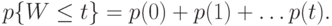 |
( 13.51) |
Вероятности состояния 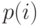 вычисляются наиболее точно, с помощью рекурсивной формулы, основанной на уравнениях состояний (13.42) Фрея:
вычисляются наиболее точно, с помощью рекурсивной формулы, основанной на уравнениях состояний (13.42) Фрея:
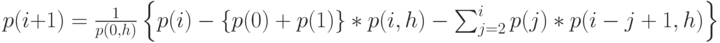 |
( 13.52) |
Для несоставных времен ожидания можно выразить распределение времени ожидания с помощью комбинации составных времен ожидания.
Если мы примем 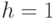 , то (13.50) может быть биноминальным разложением, записанным с помощью степени
, то (13.50) может быть биноминальным разложением, записанным с помощью степени  , где
, где  - целое число,
- целое число, 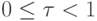 .
.
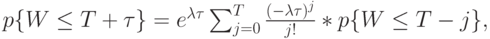 |
( 13.53) |
где 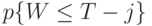 определяется в (13.51).
определяется в (13.51).
Очень точная числовая оценка может быть получена при использовании (13.51), (13.52) и (13.53).
Вероятности состояния: M/D/n
При выводе уравнений состояния Фрея (13.41) мы получаем больше комбинаций:
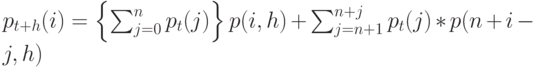 |
( 13.54) |
При условии статистического равновесия 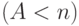 можно вычислить абсолютные моменты времени выхода из состояния:
можно вычислить абсолютные моменты времени выхода из состояния:
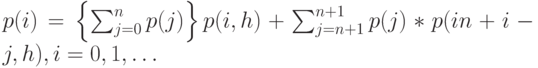 |
( 13.55) |
Если мы знаем первые n вероятности состояний  , система уравнений (13.55) может быть решена непосредственно подстановкой. Практически мы можем получить числовые значения, подставляя приблизительный набор значений для
, система уравнений (13.55) может быть решена непосредственно подстановкой. Практически мы можем получить числовые значения, подставляя приблизительный набор значений для  . Затем, заменяя эти значения, согласно рекурсивной формуле (13.55), получаем новые значения. После нескольких приближений мы получим точные результаты.
. Затем, заменяя эти значения, согласно рекурсивной формуле (13.55), получаем новые значения. После нескольких приближений мы получим точные результаты.
Явное математическое решение может быть получено с помощью производящих функций (Erlang [11] стр. 75 (83)).