|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Прикладная теория организации очередей
Дисциплина организации очереди, сохраняющая работу
Ранее мы предполагаем, что время обслуживания клиента не зависит от дисциплины организации очереди. Пропускная способность обслуживающего прибора также предполагается постоянной и не зависит, например, от длины очереди. Дисциплина организации очереди является сохраняющей работу.
На практике это не всегда происходит именно так. Если "обслуживающий прибор" - человек, скорость обслуживания часто будет увеличиваться с длиной очереди, и после некоторого времени "прибор" может устать и уменьшить скорость обслуживания.
Введём две функции, которые широко применяются в теории организации очереди.
Функция нагрузки 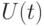 обозначает время, которое требуются, чтобы обслужить клиентов, прибывших в систему в момент времени
обозначает время, которое требуются, чтобы обслужить клиентов, прибывших в систему в момент времени  (рис. 13.2). Одновременно с поступлением вызова
(рис. 13.2). Одновременно с поступлением вызова 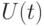 увеличивается скачком на величину времени обслуживания поступившего вызова, а между поступлением вызовов
увеличивается скачком на величину времени обслуживания поступившего вызова, а между поступлением вызовов 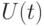 уменьшается линейно с наклоном -1 до нуля и остается нулевой до прибытия следующего вызова. Средняя величина
уменьшается линейно с наклоном -1 до нуля и остается нулевой до прибытия следующего вызова. Средняя величина
Если мы обозначим время интервала 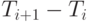 через
через 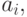 то получим
то получим 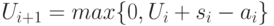 ,
,
функции нагрузки обозначается 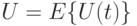 . В системе организации очереди
. В системе организации очереди 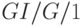 функция
функция 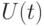 будет независима от дисциплины организации очереди, если обработка информации сохраняет время обслуживания.
будет независима от дисциплины организации очереди, если обработка информации сохраняет время обслуживания.
Виртуальное время ожидания W(t) обозначает время ожидания
клиента, если вызов поступает в момент  . Виртуальное время ожидания
. Виртуальное время ожидания  зависит от организации очереди. Средняя величина обозначена
зависит от организации очереди. Средняя величина обозначена  . Если дисциплина очереди - FCFS, то
. Если дисциплина очереди - FCFS, то 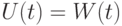 .
.
Когда мы рассматриваем Пуассоновские потоки вызовов, виртуальное время ожидания будет равно фактическому времени ожидания (свойство PASTA: математическое ожидание времени равно математическому ожиданию вызова).
Теперь рассмотрим функцию нагрузки в случайный момент времени  . Она состоит из вклада
. Она состоит из вклада  от времени, оставшегося от обслуживания обслуживаемого клиента, если таковые вообще имеются, и вклада от клиентов, ждущих в очереди. Средняя величина
от времени, оставшегося от обслуживания обслуживаемого клиента, если таковые вообще имеются, и вклада от клиентов, ждущих в очереди. Средняя величина 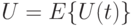 равна:
равна:
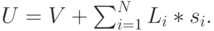
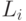 - длина очереди для клиентов типа
- длина очереди для клиентов типа  . Применяя формулу Литтла, получаем:
. Применяя формулу Литтла, получаем:
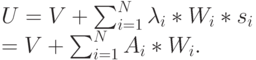 |
( 13.20) |
Как было сказано выше,  независима от дисциплины организации очереди (предполагается, что система - с сохранением работы), и
независима от дисциплины организации очереди (предполагается, что система - с сохранением работы), и  определяется выражением (13.17) для неприоритетных дисциплин организации очереди.
определяется выражением (13.17) для неприоритетных дисциплин организации очереди.
 получен в предположении дисциплины FCFS, тогда мы имеем
получен в предположении дисциплины FCFS, тогда мы имеем 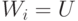 :
:
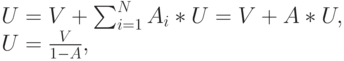 |
( 13.21) |
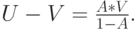 |
( 13.22) |
Согласно этим общим предположениям, подставляя (13.22) в (13.20), мы получим закон сохранения Клейнрока (1964 [65] ).
Теорема 13.2. Закон сохранения Клейнрока:
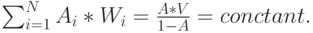 |
( 13.23) |
Среднее время ожидания для всех классов взвешенной нагрузки является независимым от дисциплины очереди.
Заметьте, что это справедливо только для неприоритетных дисциплин организации очереди. Мы можем выбрать соотношение клиентов с низким временем ожидания, не увеличивая очень среднее время ожидания остающихся клиентов. В соответствии с различными стратегиями можно распределить времена ожидания отдельным клиентам согласно нашему предпочтению.
Приоритетная дисциплина организации очереди без прерывания обслуживания
До этого мы рассматривали приоритетные системы организации очереди для  , где клиенты разделены на
, где клиенты разделены на  приоритетных классов так, чтобы клиент p имел более высокий приоритет, чем клиенты
приоритетных классов так, чтобы клиент p имел более высокий приоритет, чем клиенты 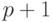 , и имел право на прерывание процесса обслуживания низкоприоритетного клиента. В рассматриваемой ниже системе это обслуживание не прерывается. Предполагается, что клиенты в классе
, и имел право на прерывание процесса обслуживания низкоприоритетного клиента. В рассматриваемой ниже системе это обслуживание не прерывается. Предполагается, что клиенты в классе  имеют среднее время обслуживания
имеют среднее время обслуживания 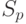 и интенсивность прибытия
и интенсивность прибытия 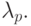 В секции 13.4.1 мы получили
В секции 13.4.1 мы получили 
Полное среднее время ожидания 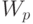 клиента класса
клиента класса  может быть вычислено непосредственно, учитывая следующие три вклада:
может быть вычислено непосредственно, учитывая следующие три вклада:
- остаточное время обслуживания
 для обслуживаемого клиента;
для обслуживаемого клиента; -
время ожидания, из-за клиентов, стоящих в очереди с приоритетом
 или выше, который находятся уже в очередях (формула Литла):
или выше, который находятся уже в очередях (формула Литла): .
. -
время ожидания из-за клиентов с более высоким приоритетом, которые поступают по ходу его ожидания:
 .
.
Всего мы имеем:
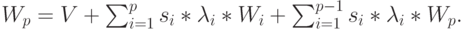 |
( 13.24) |
Для клиентов класса 1, которые имеют самый высокий приоритет, предполагая дисциплину обслуживания FCFS, мы имеем:
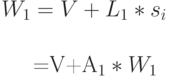 |
( 13.25) |
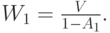 |
( 13.26) |
 - остаточное время обслуживания для клиента, когда поступает вызов от клиента, которого мы рассматриваем (13.18):
- остаточное время обслуживания для клиента, когда поступает вызов от клиента, которого мы рассматриваем (13.18):
 |
( 13.27) |
где 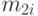 - второй момент распределения времени обслуживания i-того класса.
- второй момент распределения времени обслуживания i-того класса.
Для клиента класса 2 находим:
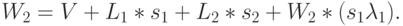
Подставляя  (13.25), находим:
(13.25), находим:
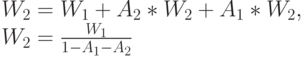 |
( 13.28) |
 |
( 13.29) |
Находим общее время ожидание (Cobham, 1954 [14] ):
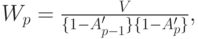 |
( 13.30) |
где:
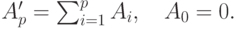 |
( 13.31) |
Формула (13.30) может быть интерпретирована следующим образом. Полное время ожидания клиентов класса  не зависит класса клиентов, ожидающих, пока обработка очереди не будет закончена {V для всех классов одинаково}.
не зависит класса клиентов, ожидающих, пока обработка очереди не будет закончена {V для всех классов одинаково}.
Кроме того, время ожидания включает время ожидания клиентов, которые уже прибыли и имеют, по крайней мере, такой же приоритет 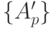 , а также клиентов с более высоким приоритетом, прибывающим в течение времени ожидания
, а также клиентов с более высоким приоритетом, прибывающим в течение времени ожидания 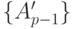
Пример 13.4.1: Система с программным управлением
Мы рассматриваем компьютер, который обслуживает два типа клиентов. Первый тип имеет постоянное время обслуживания 0,1с. и интенсивность поступления 1 вызов/сек. Другой тип имеет экспоненциально распределенное время обслуживания со средней величиной 1,6 с. и интенсивность поступления 0,5 клиента/с.
Нагрузка от двух клиентов типов тогда - 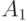 = 0,1 Эрл., соответствен-но
= 0,1 Эрл., соответствен-но 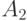 = 0,8 Эрл.
= 0,8 Эрл.
Из (13.27) мы находим:
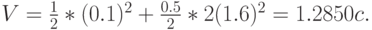
Без какого-либо приоритета среднее время ожидания по формуле Полячека-Хинчина (13.2) равно:
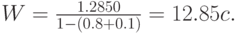
С приоритетом без прерывания процесса обслуживания находим:
Тип 1 (самый высокий приоритет)
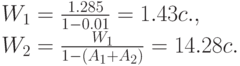
Тип 2 (высокий приоритет):
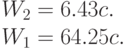
Это показывает, что мы можем изменять тип 1, почти не влияя на тип 2. Однако обратное утверждение не имеет места. Константа в законе Сохранения (13.23) такая же, как в дисциплине без приоритета.
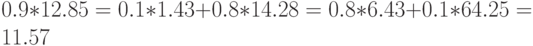
Дисциплина организации очереди SJF: M/G/1
Одно из основных свойств дисциплины организации очереди SJF: чем короче время обслуживания клиента, тем выше его приоритет. Вводя бесконечное число приоритетных классов, мы получаем из формулы (13.30), что клиент со временем обслуживания  имеет среднее время ожидания
имеет среднее время ожидания 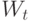 (Phipps 1956):
(Phipps 1956):
 |
( 13.32) |
где  - нагрузка от клиентов со временем обслуживания меньше или равным
- нагрузка от клиентов со временем обслуживания меньше или равным  .
.
SJF -дисциплина в результате приводит к наименьшему времени ожидания. При ожидании различные приоритетные классы имеют различные затраты в единицу времени. Клиенты класса  имеют среднее время обслуживания
имеют среднее время обслуживания 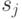 и платят
и платят 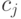 за единицу времени ожидания. Оптимальная стратегия (минимальная стоимость) состоит в том, чтобы назначить приоритеты 1, 2, … согласно увеличивающемуся отношению
за единицу времени ожидания. Оптимальная стратегия (минимальная стоимость) состоит в том, чтобы назначить приоритеты 1, 2, … согласно увеличивающемуся отношению 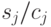 .
.
Пример 13.4.2: M/M/1 с дисциплиной очереди SJF
Мы полагаем, что случай с экспоненциально распределенными временами пребывания в системе со средней величиной 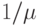 , которая оговорена, выбран как единица времени (
, которая оговорена, выбран как единица времени ( 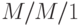 ). Заметим, что очень длительные времена обслуживания, даже когда их немного, все равно вносят значительный вклад в полную нагрузку (рис.3.2).
). Заметим, что очень длительные времена обслуживания, даже когда их немного, все равно вносят значительный вклад в полную нагрузку (рис.3.2).
Вклад в полную нагрузку от клиентов со временем обслуживания 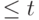 - это {(3.22), умноженное на
- это {(3.22), умноженное на 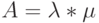 }:
}:
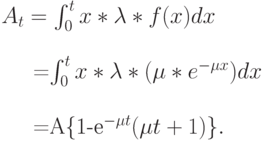
Подставляя это в (13.32), находим 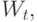 как это проиллюстрировано на рис. 13.3, где показана FCFS -стратегия. Она имеет такое же среднее время ожидания, как LCFS и SIRO, показанное для сравнения как функция фактического времени пребывания в системе.
как это проиллюстрировано на рис. 13.3, где показана FCFS -стратегия. Она имеет такое же среднее время ожидания, как LCFS и SIRO, показанное для сравнения как функция фактического времени пребывания в системе.
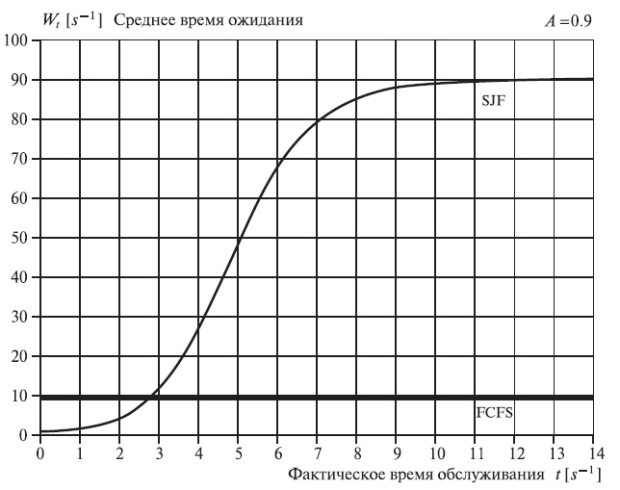
Рис. 13.3. Среднее время ожидания Wt как функция фактического времени обслуживания в M/M/1 системе для SJF- и FCFS-дисциплин, соответственно.
Среднее время ожидания для всех клиентов с SJF - меньше, чем с FCFS, но это не очевидно из рисунка. Среднее время ожидания для SJF равно:
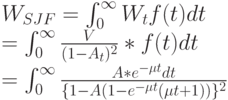
Это выражение вычислить не просто.
Предложенная нагрузка - 0,9 Эрл, и как единица времени выбрано среднее время обслуживания. Заметьте, что для SJF минимальное среднее время ожидания является 0,9 единиц времени, потому что вероятная предыдущая обслуживаемая работа должна быть закончена. Максимальное среднее время ожидания - 90 единиц времени. По сравнению с FCFS, при использовании SJF 93,6 % заданий имеют более короткое среднее время ожидания. Это относится к заданиям со временем обслуживания, меньшим, чем 2,747 средних значений времени обслуживания (единицы времени). Предложенная нагрузка может быть больше, чем один Эрл, но тогда только более короткие задания будут иметь конечное время ожидания
M/M/n приоритетная дисциплина организации очереди без прерывания обслуживания
Мы можем также обобщить классическую систему времени ожидания Эрланга 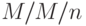 на приоритетную дисциплину организации очереди без прерывания обслуживания. При этой дисциплине все классы клиентов имеют одно и то же экспоненциальное распределение времени обслуживания со средней величиной
на приоритетную дисциплину организации очереди без прерывания обслуживания. При этой дисциплине все классы клиентов имеют одно и то же экспоненциальное распределение времени обслуживания со средней величиной 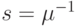 . Обозначая интенсивность прибытия на класс
. Обозначая интенсивность прибытия на класс 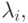 мы имеем среднее время ожидания
мы имеем среднее время ожидания  на класс
на класс  :
:
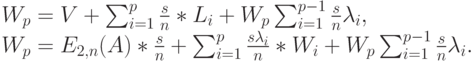
 - полная предложенная нагрузка для всех классов. Вероятность
- полная предложенная нагрузка для всех классов. Вероятность 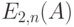 для времени ожидания определяется C-формулой Эрланга, обслуживание клиентов завершается со средним временем между окончаниями обслуживания
для времени ожидания определяется C-формулой Эрланга, обслуживание клиентов завершается со средним временем между окончаниями обслуживания  , когда все обслуживающие приборы заняты. Для самого высокого приоритетного класса
, когда все обслуживающие приборы заняты. Для самого высокого приоритетного класса  находим:
находим:
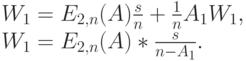 |
( 13.33) |
Для  подобным способом находим:
подобным способом находим:
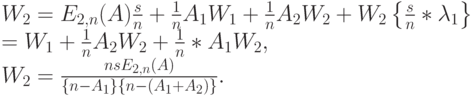 |
( 13.34) |
В общем случае находим (Cobham, 1954 [14] ):
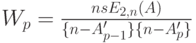 |
( 13.35) |
Дисциплина организации очереди с приоритетным возвращением к работе
Рассмотрим случай, когда продолжающееся обслуживание прервано прибытием клиента с более высоким приоритетом. После того как новый вызов будет обслужен, работа по обслуживанию прерванного вызова продолжается с того места, где оно было прервано. Эта ситуация типична для компьютерных систем. Для клиента с приоритетом  клиенты с более низким приоритетом не существуют. Среднее время ожидания
клиенты с более низким приоритетом не существуют. Среднее время ожидания 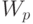 для клиента в классе
для клиента в классе  состоит из двух вкладов.
состоит из двух вкладов.
a) Время ожидания из-за клиентов с более высоким или тем же самым приоритетом, которые уже находится в очереди. Это время ожидания определяется как время ожидания клиентом в системе без приоритета, где существуют только первые  классов:
классов:
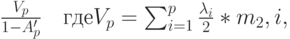 |
( 13.36) |
Оно является остающимся временем обслуживания из-за клиентов с более высоким или тем же самым приоритетом, и 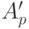 определяется (13.31).
определяется (13.31).
б) Время ожидания из-за клиентов с более высоким приоритетом, вызовы от которых поступают в течение время ожидания или во время обслуживания клиента, которого мы рассматриваем:
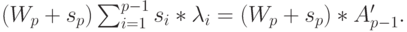
Таким образом, мы имеем:

Это может быть представлено следующим образом:
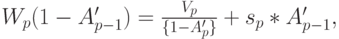
В результате получается:
 |
( 13.37) |
Тем же самым способом, как в секции 13.4.4, мы можем получить формулу для среднего времени ожидания для SJF дисциплины организации очереди с приоритетным возвращением к работе. Полное время реакции будет равно:
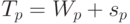 |
( 13.38) |