НОУ ИНТУИТ | Разработка телетрафика и планирование сетей. Лекция 12: Планирование телекоммуникационных сетей

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 20.04.2011 | Доступ: свободный | Студентов: 1059 / 208 | Оценка: 4.36 / 4.36 | Длительность: 22:21:00

Тема: Сетевые технологии

Специальности: Администратор коммуникационных систем, Архитектор программного обеспечения

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Планирование сети включает в себя проектирование, оптимизацию и поддержку функционирования телекоммуникационных сетей. В этой лекции мы рассмотрим технические аспекты сетевого планирования нагрузки. В секции 11.1 вводятся матрицы нагрузки и фундаментальный метод двойных коэффициентов (метод Круитгофа) для того, чтобы обновлять матрицы нагрузки согласно прогнозам. Матрица нагрузки содержит основную информацию для выбора топологии сети (секция. 11.2) и маршрутизации нагрузки (секция 11.3). В секции 11.4 мы рассматриваем приблизительное вычисление вероятностей блокировки "из конца в конец" и описываем метод фиксированной точки Эрланга (метод уменьшенной нагрузки). В секции 11.5 этот метод применяет алгоритм свертки, изложенный в Лекции 10, для вычисления блокировки "из конца в конец" в сети с виртуальной коммутацией каналов и прямой маршрутизацией. Модель позволяет рассматривать мультислото-вую BPP -нагрузку с минимальным и максимальным распределением. Та же самая модель может быть применена к иерархическим сотовым подвижным сетям связи с накладывающимися ячейками и к оптическим WDM -сетям. В секции 11.6 рассматриваются механизмы сервисной защиты. Наконец, в Секции 11.7 обсуждается оптимизация телекоммуникационных сетей с применением принципа Мо.

Ключевые слова: матрица, подстанция, сеть, функция предложения, ALOHA, PCT, дифференцирование, множители Лагранжа

Матрицы нагрузки

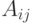Для того чтобы определить нагрузку в заданной области с станциями, мы должны знать значения $A_{ij}$ нагрузки ( 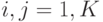i, j=1, K ), как это дано в матрице нагрузки, показанной в таблице 11.1. Матрица нагрузки предполагает, что мы знаем зоны нахождения станций. Зная матрицу нагрузки, получаем следующие две взаимозависимых задачи:

выбрать топологию сети (какие станции должны быть связаны между собой?);
выбрать принцип маршрутизации нагрузки (как мы эксплуатируем данную топологию?).

Матрица нагрузки имеет следующие элементы:

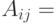$A_{ij} =$ - нагрузка от станции до станции ;

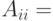$A_{ii} =$ - внутренняя нагрузка станции ;

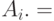A_i.= - полная исходящая нагрузка от ;

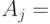A_j = - полная входящая нагрузка к .

Таблица 11.1. Матрица нагрузки. Полная входящая нагрузка равна полной исходящей нагрузке
От станции	К станции 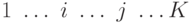$\begin{matrix} 1 & \dots &i& \dots &j& \dots K \end{matrix}$	$A_{i \cdot}=\sum_{k=1}^k A_{ik}$
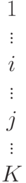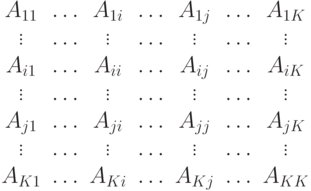$\begin{matrix} 1 \\ \vdots\\ i\\ \vdots\\ j\\ \vdots \\ K \end{matrix}$	$\begin{matrix} A_{11}& \dots & A_{1i} & \dots & A_{1j}& \dots & A_{1K} \\ \vdots & \dots & \vdots & \dots & \vdots & \dots & \vdots\\ A_{i1} & \dots & A_{ii} & \dots & A_{ij} & \dots & A_{iK}\\ \vdots & \dots & \vdots & \dots & \vdots & \dots & \vdots\\ A_{j1} & \dots & A_{ji} & \dots & A_{jj} & \dots & A_{jK}\\ \vdots & \dots & \vdots & \dots & \vdots & \dots & \vdots\\ A_{K1} & \dots & A_{Ki} & \dots & A_{Kj} & \dots & A_{KK} \end{matrix}$	$\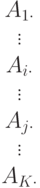begin{matrix} A_{1 \cdot} \\ \vdots\\ A_{i \cdot}\\ \vdots\\ A_{j \cdot}\\ \vdots \\ A_{K \cdot} \end{matrix}$
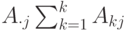$A_{\cdot j}\sum_{k=1}^kA_{kj}$	$\begin{matrix} A_{\cdot 1}& \dots &A_{\cdot i}& \dots & A_{\cdot j}& \dots & A_{\cdot K} \end{matrix}$	$\sum_{i=1}^k A_{i \cdot}=\sum_{j=1}^k A_{\cdot j}$

11.1.1 Метод двойных коэффициентов Круитгофа

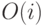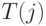Предположим, что мы знаем фактическую матрицу нагрузки, и что имеем прогноз будущей суммы -той строки O(i) и сумму -ого столбца T(j) , то есть полные входящую и исходящую нагрузки для каждой станции. Этот прогноз нагрузки может быть получен из абонентских прогнозов на отдельные станции. Посредством метода двойных коэффициентов Круитгофа (Kruithof,, 1937 [69] ) можно оценить отдельные будущие значения 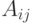$A_{ij}$ матрицы нагрузки. Процедура должна корректировать отдельные значения 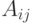$A_{ij}$ так, чтобы они были согласованы, т.е. прогнозируемые суммы строк (столбцов):

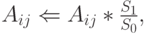$A_{ij} \Leftarrow A_{ij}*\frac{S_1}{S_0},$

( 11.1)

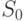где S_0 - фактическая (измеренная) сумма, и 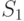S_1 - новая (прогнозируемая) сумма строки (столбца). Если мы начинаем с регулировки 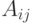$A_{ij}$ относительно сумм строки, то суммы будущих строк будут совпадать с прогнозируемыми значениями, но суммы столбцов не будут согласованы с требуемыми значениями. Поэтому следующий шаг должен корректировать полученные значения 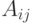$A_{ij}$ относительно сумм столбцов так, чтобы они были согласованы. Но это может привести к тому, что суммы строк снова будут расходиться. В общем случае делается несколько итераций определения сумм строк и столбцов, после чего полученное значение после нескольких повторений сходится к одному значению. Процедуру лучше всего проиллюстрировать примером, который приведен ниже.

Пример 11.1.1: Приложение метода двойных коэффициентов Круитгофа

Мы рассматриваем телекоммуникационную сеть, имеющую две станции. Матрица предлагаемой нагрузки имеет следующий вид:

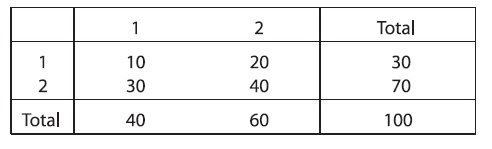
Прогноз для полного значения нагрузки, отображающий начальную и конечную нагрузку для каждой станции, показан в этой матрице:

Задача состоит в том, чтобы оценить отдельные значения матрицы посредством метод метода двойного коэффициента.

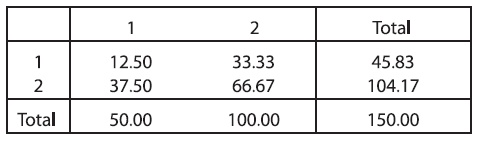
Итерация 1. Коррекция суммы строки. Мы умножаем первую строку на 45/30, а вторую строку - на 105/70.

Суммы строк теперь правильны, т.е. удовлетворяют значениям прогноза, но суммы столбцов не совпадают с заданными значениями.

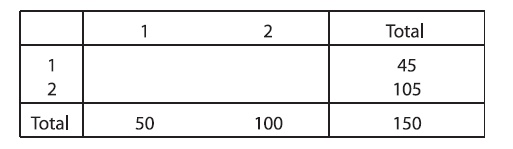
Итерация 2. Коррекция суммы столбца.

Умножаем значения первого столбца исходной матрицы на 50/60, а второго столбца - на 100/90.

Мы теперь имеем правильные суммы столбца, тогда как суммы строки немного отклоняются. Мы продолжаем, поочередно регулируя суммы столбцов и строк.

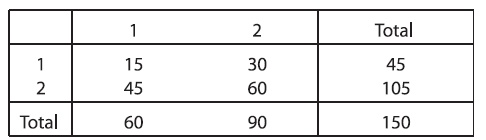
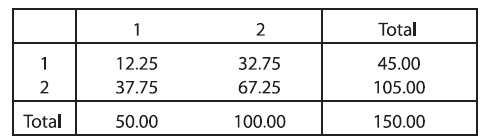
Итерация 3.

Умножаем элементы первой строки на 45/45,83, а элементы второй строки - на 105/104,17.

Мы теперь имеем правильные суммы строки, в то время как суммы столбца немного отклоняются от желательных значений. Мы продолжаем, поочередно корректировку сумм столбцов и строк:

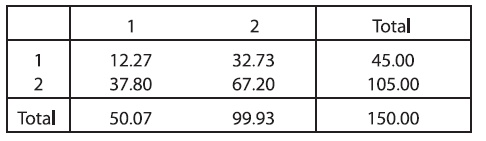
Итерация 4.

Умножаем значения первого столбца исходной матрицы на 50/50,07, а второго столбца - на 100/99,93:

После того, как выполнены четыре итерации, суммы и строк и столбцов приближаются (в данном случае совпадают) к прогнозируемым числам. Есть другие методы для оценки будущих отдельных значений нагрузки 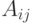$A_{ij}$ , но метод двойных коэффициентов Круитгофа имеет некоторые важные свойства (Нести, 1988 [5] ).

Уникальность. Для заданного прогноза существует только одно решение.
Обратимость. Финальная матрица может быть полностью приведена к начальной матрице с помощью той же самой процедуры.
Транзитивность. Финальная матрица - та же самая независимо от того, получена ли она с помощью одного шага или с помощью ряда промежуточных преобразований, (например, один 5-летний прогноз или пять 1-летних прогнозов дают одинаковый результат).
Постоянство результата не зависит от нумерации станций. Мы можем изменить нумерацию станций в матрице, не влияя на конечный результат.
Разбиение и объединение. Отдельные станции могут быть разбиты на подстанции или объединены в большие станции, не влияя на результаты расчетов. Это свойство для метода двойных коэффициентов Круитгофа не выполняется точно, но отклонения достаточно малы.

Топология

В Лекции 1 мы описали основную топологию сети: звездная сеть, узловая сеть, кольцевая сеть, иерархическая сеть и неиерархическая сеть.

Принципы маршрутизации

Это очень большой вопрос, который включает такие разделы, как альтернативная маршрутизация нагрузки, выравнивание нагрузки и т. д. В (Ash, 1998 [3] ) есть детальное описание этих вопросов.

Приблизительные методы вычисления значений блокировки "из конца в конец".

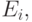Если предположить, что линии связи на сети обслуживаются независимо, то вероятность блокировки из "конца в конец" вычисляется просто. Это делается с применением классической формулы, мы вычисляем вероятность блокировки каждой линии связи. Если мы примем вероятность блокировки линии связи равной E_i, то можем вычислить вероятность блокировки из "конца в конец" для попытки вызова по всему маршруту следующим образом:

$E_j=1-\Pi_{i \in R}(1-E_i),$

( 11.2)

где - набор линий связи, включенных в маршрут вызова. Это значение будет худшим случаем, потому что блокировка на каждой линии связи уменьшает нагрузку на следующем шаге и поэтому потери на последней линии связи маршрута меньше.

Для малых вероятностей блокировки мы имеем:

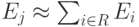$E_j \approx \sum_{i \in R} E_i$

( 11.3)

Метод фиксированной точки

Вызов обычно занимает каналы на большем количестве отрезков маршрута, и вообще нагрузка на отдельных линиях связи сети будет коррелированная. Вероятность блокировки на отдельных линиях связи при попытке установления вызова поэтому также будет коррелированная. Метод фиксированной точки Эрланга является попыткой принять во внимание это свойство.

Точный метод расчета блокировки "из конца в конец"

Телекоммуникационные сети коммутации каналов с прямой маршрутизацией имеют такую же сложность, что и сети с организацией большого числа цепочек очередей (секция 14.9) и (табл. 14.3). Необходимо сохранить в памяти число занятых каналов для каждого соединения. Поэтому максимальное число состояний будет равно:

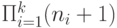$\Pi_{i=1}^k(n_i+1)$

( 11.4)

Таблица 11.2. В телекоммуникационных сетях коммутации каналов с прямой маршрутизацией $d_{ij}$ обозначает размер слота (запрос пропускной способности) маршрута на соединение (см. табл. 14.3)
Соединение	Маршрут $\begin{matrix} 1&2& \dots & N \end{matrix}$	Число каналов
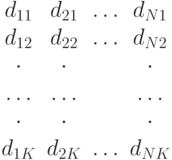$\begin{matrix} 1\\ 2\\ \cdot\\ \dots\\ \cdot\\ K \end{matrix}$	$\begin{matrix} d_{11}&d_{21}& \dots & d_{N1}\\ d_{12}& d_{22}& \dots & d_{N2}\\ \cdot & \cdot & & \cdot\\ \dots & \dots & & \dots\\ \cdot & \cdot & & \cdot\\ d_{1K& d_{2K}& \dots & d_{NK} \end{matrix}$	$\begin{matrix} n_1\\ n_2\\ \cdot\\ \dots\\ \cdot\\ n_K \end{matrix}$

Алгоритм свертки

Алгоритм свертки, описанный в Лекции 10, может непосредственно быть применен к сетям с прямой маршрутизацией, потому что к среде маршрутов применима мультиплекативная форма. Свертка становится многомерной, размерность это число соединений в сети. Усечение пространства состояний становится более сложным, и число состояний очень увеличивается.

Управление нагрузкой и защита сервиса

В телекоммуникационных сетях со многими пользователями, конкурирующими за одни и те же ресурсы (многостанционный доступ), важно определить сервисные требования пользователей и гарантировать, что при нормальных сервисных условиях будет обеспечен класс обслуживания (GoS). В большинстве систем это может быть обеспечено тем, что льготные абоненты (полицейские, медицинские услуги и т.д.) получают более высокий приоритет, чем обычные абоненты, когда они делают попытки вызова. При нормальных условиях мы хотим гарантировать, что для всех абонентов и для всех типов вызовов (местный, внутренний, международный) приблизительно обеспечивается один и тот же уровень обслуживания, например, блокировка - 1%.

При некоторых ситуациях попытки вызова определенных групп абонентов не должны блокироваться полностью, а другие группы в то же самое время получают большое число отказов. Это предполагает "коллективное наказание" второй группы абонентов.

Исторически оно возникло из-за децентрализованной структуры и применения ограниченной доступности (транспонировании), которые с точки зрения сервисной защиты все еще являются применимыми и полезными.

Цифровые системы и сети имеют увеличенную сложность, и без профилактических мер обслуженная нагрузка, функция предложенной нагрузки будет типично иметь форму, подобную системе ALOHA (рис.6.4).

Чтобы гарантировать, что система во время перегрузки будет продолжать работать c максимальной производительностью, применяются различные стратегии. В системах (станциях) с программным управлением мы можем применять введение промежутков между вызовами ( call-gapping ) и распределение приоритетов для задач (Лекции 13).

В телекоммуникационных сетях общими являются две стратегии: резервные каналы и защита виртуальных каналов.

Дальше >>

Авторизоваться

Разработка телетрафика и планирование сетей

Планирование телекоммуникационных сетей