|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Построение тестов с использованием алфавитов большой значности
20.2. Построение тестов в шестнадцатизначном алфавите
Как уже отмечалось выше, повышение мощности алфавита позволяет в некоторых случаях снять неопределенность в схеме и тем самым ускорить генерацию теста.
Это в наибольшей степени относится к алфавиту 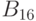 [20.1,20.4-20.6]. Рассмотрим особенности выполнения основных этапов генерации тестов в универсальном алфавите
[20.1,20.4-20.6]. Рассмотрим особенности выполнения основных этапов генерации тестов в универсальном алфавите 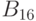 . Сначала, на этапе препроцессорной обработки, целесообразно, насколько это возможно, снять неопределенность, используя только структурные свойства схемы и значение местоположения неисправности, то есть, выполнить так называемую структурную импликацию. Алфавит
. Сначала, на этапе препроцессорной обработки, целесообразно, насколько это возможно, снять неопределенность, используя только структурные свойства схемы и значение местоположения неисправности, то есть, выполнить так называемую структурную импликацию. Алфавит 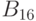 представляет для этого большие возможности, чем остальные алфавиты, рассмотренные выше.
представляет для этого большие возможности, чем остальные алфавиты, рассмотренные выше.
Рассмотрим это на примере схемы, изображенной на рис. 20.1 для неисправности 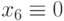 . Сначала полагаем
. Сначала полагаем  .
Как и в предыдущем примере, схема имеет один выход, поэтому полагаем
.
Как и в предыдущем примере, схема имеет один выход, поэтому полагаем 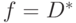 . Однако, здесь существует два пути от места неисправности до выхода схемы и заранее неизвестно, какой из них будет активизирован. Поэтому полагаем
. Однако, здесь существует два пути от места неисправности до выхода схемы и заранее неизвестно, какой из них будет активизирован. Поэтому полагаем  ,
, 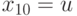 .
На все остальные элементы неисправность не оказывает влияния и поэтому
.
На все остальные элементы неисправность не оказывает влияния и поэтому 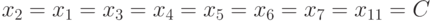 .
.
Таким образом, в процессе структурной импликации нужно выполнить следующие действия.
- Внести неисправность (значения
 или
или 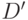 ), в зависимости от типа неисправности на неисправной линии).
), в зависимости от типа неисправности на неисправной линии).
- Присвоить
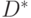 всем линиям схемы, которые должны изменить свое значение при наличии неисправности.
всем линиям схемы, которые должны изменить свое значение при наличии неисправности.
- Присвоить С всем линиям, значение на которых не может измениться при данной неисправности.
- Присвоить
 всем остальным линиям.
всем остальным линиям.
Кроме этого, на данном этапе можно некоторые линии схемы искусственно установить в определенные значения. Особенно это важно в интерактивных системах построения тестов, где человек-оператор принимает непосредственное участие в генерации теста. Оператор может, исходя из своего опыта, установить некоторые линии схемы в определенные значения, необходимые или желательные для построения теста.
Начальное присваивание выполняется безотносительно функций логических элементов. Учет свойств логических элементов в алфавите 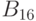 позволяет эффективно выполнять процедуры импликации. Рассмотрим сначала прямую импликацию. Она может быть выполнена с помощью системы функций
позволяет эффективно выполнять процедуры импликации. Рассмотрим сначала прямую импликацию. Она может быть выполнена с помощью системы функций 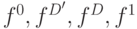 [20.1,20.6], рассмотренной в
"Система многозначных алфавитов и функций"
.
Эти функции позволяют проводить моделирование в алфавите
[20.1,20.6], рассмотренной в
"Система многозначных алфавитов и функций"
.
Эти функции позволяют проводить моделирование в алфавите 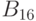 , к которому, собственно, и сводится прямая импликация. Кроме этого необходимо выполнить пересечение кодов значений сигналов до и после импликации. Рассмотрим элемент конъюнкции
, к которому, собственно, и сводится прямая импликация. Кроме этого необходимо выполнить пересечение кодов значений сигналов до и после импликации. Рассмотрим элемент конъюнкции 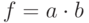 , находящийся в некоторой схеме. Пусть в результате предыдущих действий его входы и выход имеют соответствующие значения:
, находящийся в некоторой схеме. Пусть в результате предыдущих действий его входы и выход имеют соответствующие значения: 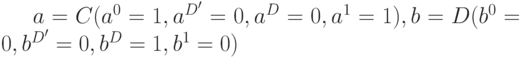 и
и 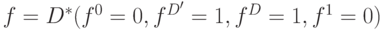 . С помощью функций
. С помощью функций 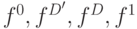 для вентиля И получаем новые значения
для вентиля И получаем новые значения 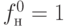 ,
,
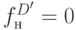 ,
,
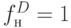 ,
,
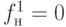 .
Далее, выполнив пересечение кодов старых и новых значений путем покомпонентной конъюнкции, получим
.
Далее, выполнив пересечение кодов старых и новых значений путем покомпонентной конъюнкции, получим
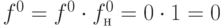 ,
,
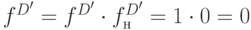 ,
,
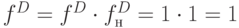 ,
,
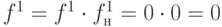 .
Таким образом, в результате импликации неопределенность на выходе уменьшилась до единственной комбинации значений сигналов в исправном и неисправном ДУ. Если в результате покомпонентной конъюнкции получается символ
.
Таким образом, в результате импликации неопределенность на выходе уменьшилась до единственной комбинации значений сигналов в исправном и неисправном ДУ. Если в результате покомпонентной конъюнкции получается символ
 (
(
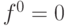 ,
,
,
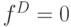 ,
,
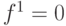 ), то это говорит о противоречивой ситуации. Аналогично прямая импликация выполняется и для других элементов.
), то это говорит о противоречивой ситуации. Аналогично прямая импликация выполняется и для других элементов.
Для выполнения обратной импликации можно также построить аналог функций 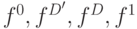 , которые позволяют проводить ее в универсальном алфавите
, которые позволяют проводить ее в универсальном алфавите 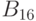 . Особенно эффективной обратная импликация является для двухвходовых элементов. В этом случае, считая заданными значение выхода и одного из входов, мы находим значение второго входа (пересекая, как и в предыдущем случае, код нового значения с кодом старого значения, по возможности уменьшаем неопределенность).
Для основных вентилей эти функции представлены в табл. 7.7. Поскольку входы вентилей симметричны, то функции для второго входа можно получить из функций для первого входа простой заменой переменной.
. Особенно эффективной обратная импликация является для двухвходовых элементов. В этом случае, считая заданными значение выхода и одного из входов, мы находим значение второго входа (пересекая, как и в предыдущем случае, код нового значения с кодом старого значения, по возможности уменьшаем неопределенность).
Для основных вентилей эти функции представлены в табл. 7.7. Поскольку входы вентилей симметричны, то функции для второго входа можно получить из функций для первого входа простой заменой переменной.
Продолжим наш пример для вентиля 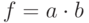 . После прямой импликации
. После прямой импликации 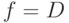 ,
,  ,
, 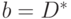 . Выполнив обратную импликацию для
. Выполнив обратную импликацию для  с помощью функций табл. 7.7 для вентиля
с помощью функций табл. 7.7 для вентиля 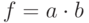 , получим
, получим 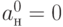 ,
,
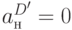 ,
,
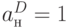 ,
,
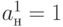 .
Далее следует, как и в случае прямой импликации, найти пересечение кодов
.
Далее следует, как и в случае прямой импликации, найти пересечение кодов 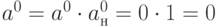 ,
,
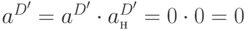 ,
,
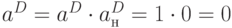 ,
,
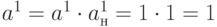 .
В данном случае неопределенность на входе
.
В данном случае неопределенность на входе  также уменьшилась до одной комбинации. Затем, считая значения
также уменьшилась до одной комбинации. Затем, считая значения  и
и  известными, следует выполнить обратную импликацию для
известными, следует выполнить обратную импликацию для  .
Получаем
.
Получаем 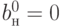 ,
,  ,
, 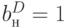 ,
, 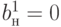 .
Пересекая со старыми значениями, получаем
.
Пересекая со старыми значениями, получаем 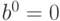 ,
, 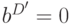 ,
, 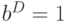 ,
, 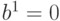 , то есть
, то есть 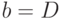 . Таким образом, в результате прямой и обратной импликации на линиях вентиля установились все определенные значения. Для булевой функции многих переменных соответствующие функции могут быть получены из ее суперпозиции через булевы функции двух переменных.
. Таким образом, в результате прямой и обратной импликации на линиях вентиля установились все определенные значения. Для булевой функции многих переменных соответствующие функции могут быть получены из ее суперпозиции через булевы функции двух переменных.
Процедуры импликации выполняются после начального присваивания и в процессе генерации теста, когда надо снять неопределенность в результате выбора некоторого пути в дереве решения. Импликация выполняется до тех пор, пока значения сигналов не установятся (неопределенность дальше можно снять только искусственно путем выбора решения). Порядок, в котором выполняется импликация, не важен для установившихся значений, но влияет на время выполнения. Здесь могут применяться различные стратегии.
В качестве примера рассмотрим схему рис. 20.1 с неисправностью 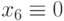 , Если мы выполним импликацию после начального присваивания, рассмотренного выше, то получим
, Если мы выполним импликацию после начального присваивания, рассмотренного выше, то получим 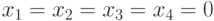 ,
, 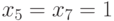 ,
,  ,
,  ,
, 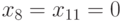 и
и 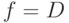 . Тo есть, в данном случае тест находится однозначно, в отличие от
. Тo есть, в данном случае тест находится однозначно, в отличие от  -алгоритма, где необходим перебор. В общем случае, конечно, полностью поиска на дереве решений нельзя избежать и в алфавите
-алгоритма, где необходим перебор. В общем случае, конечно, полностью поиска на дереве решений нельзя избежать и в алфавите  .
Но для некоторых классов схем он существенно упрощается. Кроме этого, как отмечалось выше, этот подход удобен для интерактивных систем, где оператор, задавая для некоторых линий определенные значения, облегчает задачу поиска для компьютера.
.
Но для некоторых классов схем он существенно упрощается. Кроме этого, как отмечалось выше, этот подход удобен для интерактивных систем, где оператор, задавая для некоторых линий определенные значения, облегчает задачу поиска для компьютера.
Таким образом, повышение значности алфавита позволяет точнее описывать возможные комбинации значений сигналов в исправной и неисправной схеме, что повышает эффективность алгоритмов. Алфавит 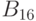 , дает максимальное разрешение (для комбинационных ДУ). Кроме того, в этом алфавите не нужна процедура
, дает максимальное разрешение (для комбинационных ДУ). Кроме того, в этом алфавите не нужна процедура  -прохода и D-граница.
Основной здесь является операция доопределения (обратная фаза). Здесь с помощью прямой импликации определяются для каждой линии схемы всевозможные комбинации значений сигналов для исправной и неисправной схемы. Таким образом, множество внешних выходов схемы, на которых может проявиться неисправность, также известны.
Это те выходы, значения сигналов для которых в алфавите
-прохода и D-граница.
Основной здесь является операция доопределения (обратная фаза). Здесь с помощью прямой импликации определяются для каждой линии схемы всевозможные комбинации значений сигналов для исправной и неисправной схемы. Таким образом, множество внешних выходов схемы, на которых может проявиться неисправность, также известны.
Это те выходы, значения сигналов для которых в алфавите  содержат
содержат  или
или 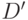 . Таким образом, задача, в основном, сводится к доопределению - поиску таких значений сигналов внешних входов ДУ, чтобы хотя бы на одном внешнем выходе из множества возможных комбинаций осталась только одно значение
. Таким образом, задача, в основном, сводится к доопределению - поиску таких значений сигналов внешних входов ДУ, чтобы хотя бы на одном внешнем выходе из множества возможных комбинаций осталась только одно значение  или
или 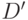 .
Существенным для быстродействия является порядок линий, для которых выполняется доопределение. Теоретические и экспериментальные исследования показывают, что наиболее эффективна стратегия, при которой сначала выполняется доопределение для линий, расположенных ближе к внешним входам (в общем случае имеющих лучшую управляемость).
.
Существенным для быстродействия является порядок линий, для которых выполняется доопределение. Теоретические и экспериментальные исследования показывают, что наиболее эффективна стратегия, при которой сначала выполняется доопределение для линий, расположенных ближе к внешним входам (в общем случае имеющих лучшую управляемость).
Ключевые термины:
Многозначный алфавит - множествосимволов, отражающих распределение сигналов в схеме.
Многозначная функция - определяется на произвольном  -значном алфавите
-значном алфавите 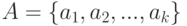 как отображение
как отображение
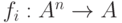 , где
, где  -число аргументов функции.
-число аргументов функции.
Краткие итоги
В лекции рассматривается построение проверяющего теста с использованием алфавитов повышенной значности.
В "Построение тестов с использованием алфавитов большой значности" описано применение 9 и 10- значного алфавита для построения тестов. Повышение значности алфавитов в некоторых случаях позволяют сократить перебор в процессе поиска решения.
В "Построение тестов с использованием алфавитов большой значности" представлен метод построения тестов, основанный на использовании универсального 16-значного алфавита. Описана импликация в 16-значном алфавите, которая часто позволяет сократить число вариантов при переборе.
Вопросы и упражнения
- Какие алфавиты повышенной значности используются для построения тестов?
- Опишите физический смысл символов 10-значного алфавита.
- Что дает использование алфавитов большей значности?
- Приведите пример построения теста в 10-значном алфавите.
- Опишите физический смысл 16-значного алфавита.
- Что такое структурная импликация?
- Какие функции используются при построении теста в 16-значном алфавите?
- Как выполняется прямая импликация в 16-значном алфавите?
- Как выполняется обратная импликация в 16-значном алфавите?
- Приведите пример построения теста в 16-значном алфавите.
