Структуры данных и алгоритмы

Для определения функций возвращения числа элементов дерева и списка элементов заданного уровня ниже используются вспомогательные функции, которые применяются к спискам деревьев.

Функция number вычисления количества вершин дерева определяется в виде:

In[66]:= number[tree[_, tl_]] := 1 + numberlist[tl]
numberlist[nil] := 0
numberlist[cons[h_,t_]]:=number[h]+numberlist[t]
number[tr]
 Out[69]= 8

Аналогичным образом определяется функция leveltree построения списка элементов уровня n дерева:

In[70]:= leveltree[tree[a_, _], 0] := cons[a, nil]
leveltree[tree[_, tl_], n_] := levellist[tl, n-1]
levellist[nil, n_] := nil
levellist[cons[h_,t_],n_]:=append[leveltree[h,n],
 levellist[t, n]]
leveltree[tr, 0]
leveltree[tr, 1]
leveltree[tr, 2]
leveltree[tr, 3]
 Out[74]= cons[1, nil]
 Out[75]= cons[2, cons[3, cons[4, nil]]]
 Out[76]= cons[5, cons[6, cons[7, nil]]]
 Out[77]= cons[8, nil]

Двумерные структуры данных

В табличных структурах данных элемент имеет два индекса - номер строки и номер столбца. Примером двумерной структуры данных является матрица.

Матрицы можно моделировать в виде списка строк, которые представлены в виде списков элементов. Например, матрицу

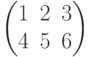
можно представить следующим образом (см. программу ниже):

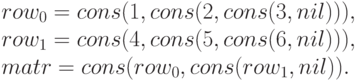
Функция get возвращения элемента матрицы с заданными индексами и функция set, которая вставляет элемент в позицию с заданными индексами, определяются следующим образом:

In[78]:= row0 := cons[1, cons[2, cons[3, nil]]]
row1 := cons[4, cons[5, cons[6, nil]]]
matrix := cons[row0, cons[row1, nil]]
get[matr_, i_, j_] := nth[nth[matr, i], j]
get[matrix, 1, 1]
 Out[82]= 5

 In[83]:= set[matr_, i_, j_, el_] := setnth[matr,
 setnth[nth[matr, i], el, j], i]
set[matrix, 1, 2, 7]
 Out[84]= cons[cons[1, cons[2, cons[3, nil]]], 
cons[cons[4, cons[5, cons[7, nil]]], nil]]

Определение функций sizeY и sizeX, которые возвращают число строк и число столбцов матрицы, соответственно, имеет вид:

In[85]:= sizeY[matr_] := length[matr]
sizeX[nil] := 0
sizeX[cons[h_, _]] := length[h]
sizeY[matrix]
sizeX[matrix]
 Out[88]= 2
 Out[89]= 3

Наконец, определим функции row и column, которые возвращают соответственно строку i и столбец j матрицы:

In[90]:= row[matr_, i_] := nth[matr, i]
column[nil, j_] := nil
column[cons[h_,t_],j_]:=cons[nth[h,j],column[t,j]]
row[matrix, 1]
column[matrix, 2]
 Out[93]= cons[4, cons[5, cons[6, nil]]]
 Out[94]= cons[3, cons[6, nil]]

Понятие алгоритма

Под алгоритмом понимается конечная система предписаний, определяющая содержание и порядок действий над исходными и промежуточными данными для получения после конечного числа шагов в качестве результата выходных данных. Алгоритм предназначен для исполнителя и описывается в его командах. Все данные, с которыми работает исполнитель, принадлежат его среде.

Алгоритмы характеризуются следующими свойствами: дискретность - действия разбиваются на конечную последовательность шагов; детерминированность - результат однозначно определяется последовательностью шагов, для одних и тех же исходных данных получается один и тот же результат; понятность - исполнитель однозначно воспринимает, а также понимает все предписания алгоритма; результативность - при точном выполнении предписаний результат получается за конечное число шагов; массовость - алгоритм правильно работает на некотором множестве исходных данных.

Для каждого исполнителя набор допустимых действий ограничен, и существуют действия, которые он выполнить не может.

Алгоритм сортировки списка вставками

Для описаний алгоритмов используются различные способы: текстовая форма, блок-схема, псевдокод и др.

Описание алгоритма зависит от исполнителя. Например, рассмотрим алгоритм сортировки списка вставками. В императивных языках программирования сортировка одномерного массива выполняется в том же массиве. В логических языках создается и возвращается новый список, который образуют упорядоченные элементы исходного списка.

Рассмотрим алгоритм сортировки списка вставками на множестве термов, представляющих списки.

На вход алгоритма подается список элементов, на выходе возвращается упорядоченный список данных элементов.

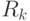Обозначим через и - текущие списки на шаге k алгоритма. На нулевом шаге положим: 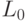- исходный список, 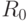- пустой список. Далее шаги алгоритма нумеруются, начиная с 1.

Шаг m. Если список 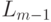пуст, то алгоритм завершается, и в качестве результата выдается список 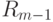. Если список 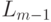не пуст, то в качестве списка берется список, полученный в результате вставки головы списка 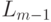в список 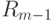так, чтобы полученный список был упорядоченным, а в качестве списка 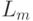берется хвост списка 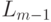. После этого выполняется переход к шагу m + 1.

Если выполняется сортировка по возрастанию элементов, то процедуру вставки в упорядоченный список R элемента a можно определить рекурсивно следующим образом: если элемент a больше головы h списка R, то возвращается список, головой которого является h, а хвостом - результат вставки элемента a в хвост списка R; в противном случае возвращается список с головой a и хвостом R.

Блок-схема алгоритма сортировки списка вставками представлена на рис. 6.6. В ней используются функции head и tail возвращения головы и хвоста списка, соответственно, а также функция ins вставки элемента в упорядоченный список. Через 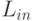обозначен входной список, а через - выходной.

Рис. 6.6. Блок-схема алгоритма сортировки вставками

Псевдокод алгоритма имеет вид:

l = [1, 2, 3], r = []
цикл пока l не пуст
r = ins(r, head(l))
l = tail(l)
конец цикла
печать r

На языке Wolfram для списков, представленных термами, алгоритм реализуется следующим образом:

In[1]:= x := cons[4,cons[2,cons[5,cons[3,cons[1,nil]]]]]
insertionsort[l_] := sort[l, nil]
sort[nil, l_] := l
sort[cons[h_, t_], l_] := sort[t, ins[h, l]]
ins[a_, nil] := cons[a, nil]
ins[a_, cons[h_, t_]] := If[a > h, 
cons[h, ins[a, t]], cons[a, cons[h, t]]]
insertionsort[x]
 Out[7]= cons[1, cons[2, cons[3, cons[4, cons[5, nil]]]]]