Структуры данных и алгоритмы
Очередь
Очередь (англ. queue) - это тип данных, в котором элементы организуются по принципу "первый пришел - первый вышел" (англ. FIFO - first in - first out). Она отличается от стека тем, что новый элемент добавляется с одной стороны - в конец очереди, а забирается с другой стороны - из начала очереди. Примером очереди является очередь на кассу в супермаркете.
Например, пусть [1, 2, 3] - очередь. Если добавить элемент 5 в конец очереди, то получится очередь [5, 1, 2, 3]. Первым элементом очереди является 3. После удаления первого элемента из очереди [5, 1, 2, 3] останется очередь [5, 1, 2].
Функция addRear добавления элемента в конец очереди определяется следующим образом:
In[42]:= addRear[p_, a_] := cons[a, p] addRear[x, 5] Out[43]= cons[5, cons[1, cons[2, cons[3, nil]]]]
Первый элемент очереди возвращает функция top, а очередь без первого элемента - функция pop, которые были определены ранее.
Дек
Дек (англ. deque) - это тип данных, который отличается от очереди тем, что в нем можно добавлять элементы как в начало, так и в конец, просматривать как первый, так и последний элемент, и удалять как первый, так и последний элемент. Поэтому дек также называют двухсторонней очередью.
Например, пусть [1, 2, 3] - дек. В результате добавления элемента 5 в начало этого дека, получится дек [1, 2, 3, 5]. В результате добавления элемента 7 в конец второго дека получится дек [7, 1, 2, 3, 5].
Указанные выше операции в виде функций на языке Wolfram были определены ранее (полный список указанных функций для деков определяется также ниже в п. 6.2.4).
Иерархические структуры данных. Деревья
Иерархическая структура данных - это организация данных, в которой элементы связаны отношением частичного порядка. Если пара несовпадающих элементов принадлежит этому отношению, то один из них находится на более высоком уровне, чем другой.
Основным примером иерархической структуры данных является конечное корневое дерево - граф без циклов, один из элементов которого является корнем. Корень образует нулевой уровень дерева. Смежные с корнем вершины образуют первый уровень, они являются потомками корня. Смежные с ними и не принадлежащие предыдущему уровню - второй уровень дерева, и так далее. Вершина a называется потомком смежной с ней вершины b, если номер ее уровня на единицу больше номера уровня вершины b.
Дерево, в котором каждая вершина имеет не более двух потомков, называется бинарным. Для представления бинарного дерева используем 0-арный символ leaf, обозначающий пустое дерево и тернарный символ bin, аргументы которого соответствуют левому поддереву, корню и правому поддереву. С помощью этих символов бинарное дерево, приведенное на рис. 6.4 (a), представляется в виде терма bin(bin(leaf, 1, leaf), 2, bin(leaf, 3, leaf)).
Произвольное дерево можно представить в виде терма с бинарным символом tree, первый аргумент которого хранит вершину дерева, а второй - список поддеревьев. Например, дереву, представленному на рис. 6.4 (b), соответствует терм tree(1, cons(tree(2, nil), cons(tree(3, nil), cons(tree(4, nil), nil)))).
Определим операции, которые возвращают корень дерева, левое и правое поддеревья для бинарных деревьев и список поддеревьев для произвольных деревьев, а также операции вычисления числа вершин дерева и списка вершин уровня n дерева.
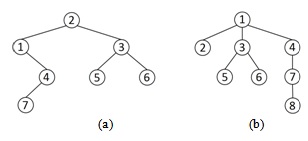
Используем в программе дерево, приведенное на рис. 6.5 (a).
Терм, представляющий бинарное дерево, а также функции возращения его корня и левого и правого поддеревьев определяются следующим образом:
In[44]:= z = bin[bin[leaf,1,bin[bin[leaf,7,leaf],4,leaf]], 2, bin[bin[leaf,5,leaf],3,bin[leaf,6,leaf]]]; rootbintree[bin[_, a_, _]] := a lefttree[bin[l_, _, _]] := l righttree[bin[_, _, r_]] := r rootbintree[z] lefttree[z] righttree[z] Out[48]= 2 Out[49]= bin[leaf, 1, bin[bin[leaf, 7, leaf], 4, leaf]] Out[50]= bin[bin[leaf, 5, leaf], 3, bin[leaf, 6, leaf]]
Функцию count вычисления количества вершин дерева можно определить рекурсивно в виде:
In[51]:= count[leaf] := 0 count[bin[l_, _, r_]] := count[l] + 1 + count[r] count[z] Out[53]= 7
Для определения функции level, возвращающей список вершин дерева уровня n, используем функцию append (см. выше):
In[54]:= level[leaf, _] := nil level[bin[_, a_, _], 0] := cons[a, nil] level[bin[l_, _, r_], n_] := append[level[l, n - 1], level[r, n - 1]] level[z, 0] level[z, 1] level[z, 2] level[z, 3] Out[57]= cons[2, nil] Out[58]= cons[1, cons[3, nil]] Out[59]= cons[4, cons[5, cons[6, nil]]] Out[60]= cons[7, nil]
Далее определяются операции для произвольных деревьев. Используется дерево, показанное на рис. 6.5 (b).
Терм, представляющий дерево, а также функции возращения его корня и списка поддеревьев определяются следующим образом:
In[61]:= tr = tree[1, cons[tree[2, nil], cons[tree[3, cons[tree[5, nil], cons[tree[6, nil], nil]]], cons[tree[4, cons[tree[7, cons[tree[8, nil], nil]], nil]], nil]]]]; root[tree[a_, _]] := a subtreelist[tree[_, tl_]] := tl root[tr] subtreelist[tr] Out[64]= 1 Out[65]= cons[tree[2, nil], cons[tree[3, cons[tree[5, nil], cons[tree[6, nil], nil]]], cons[tree[4, cons[tree[7, cons[tree[8, nil], nil]], nil]], nil]]]