База знаний Wolfram|Alpha
Система Wolfram|Alpha - база знаний, которую также называют интеллектуальной машиной знаний, использует вычислительные интеллектуальные алгоритмы для поиска ответов на онлайн-запросы. Она была создана с помощью системы компьютерной математики Wolfram Mathematica. Система Wolfram|Alpha ищет ответы в своей базе знаний и в качестве ответа выдает как результаты вычислений, так и некоторые сведения из базы знаний, которые могут иметь отношение к запросу. База содержит сведения из большого количества областей знаний. Для запросов используется язык, близкий к естественному. Когда это возможно, ответ содержит формулировку запроса на языке Wolfram.
Ниже приведены примеры запросов к базе знаний Wolfram|Alpha по рассмотренным в предыдущих главах вопросам, а также примеры аналогичных запросов в облаке Wolfram.
Запросы о представлении информации в компьютере
Представление чисел в системах счисления
Рассмотрим запросы о преобразования представлений чисел между системами счисления и о выполнении арифметических операций в системах счисления. Принадлежность числа к системе счисления указывается с помощью знака подчеркивания: запись 123_4 соответствует  .
.
Пример 1. Найти троичное представление числа  в системе Wolfram|Alpha можно с помощью запроса
в системе Wolfram|Alpha можно с помощью запроса
convert 12a.a12 from base 16 to base 3 или convert 12a.a12_16 to base 3
Ответ на запрос выдается после нажатия на клавишу Enter или на знак
. В разделе Input interpretation приводится интерпретация запроса, который будет вычисляться системой (рис. 7.1).На вкладке Plain Text см. рис. 7.1 можно увидеть вариант этого запроса на языке Wolfram:
BaseForm[16^^12a.a12, 3]
В разделе Result приводится результат вычислений:
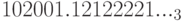
Число знаков после запятой будет увеличено при выборе команды More digits. Дополнительно система показывает результат в десятичном виде, а также в других системах счисления.
Пример 2. Запрос на преобразование из одной системы счисления в другую может быть сокращен. Например, рассмотрим запрос
43000 to base 60
Он интерпретируется так же, как и предыдущие запросы, в виде
convert 43000 to base 60
На языке Wolfram запрос имеет вид:
BaseForm[43000, 60]
Система Wolfram|Alpha приводит следующий результат:
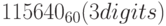
Она предлагает ответ и в нормализованном виде:  . Результат также приводится в других системах счисления.
. Результат также приводится в других системах счисления.
Пример 3. Рассмотрим запрос:
23_8 + 14_16 * 12_4
Операция умножения обозначается как символом *, так и символом пробела. Запрос интерпретируется в виде

На языке Wolfram запрос имеет вид:
8^^23 + 16^^14 4^^12
Результат 139 выдается в десятичной системе счисления, дополнительное приводится его представление в других системах счисления.
Кодирование целых и действительных чисел
Рассмотрим примеры запросов, которые в качестве дополнительной информации возвращают результаты двоичного кодирования чисел с различной точностью.
Пример 4. Пусть запрос имеет вид:
convert 34/3 to base 2
В режиме краткого ответа можно узнать, что

(по умолчанию период не выделяется).
Кроме этого, приводится преставление числа 11,(3) с двойной точностью в 16-ричном формате, при этом по умолчанию используется нумерация байт от младшего к старшему (little-endian): abaaaaaaaaaa2640.
Количество выдаваемых сведений можно регулировать с помощью команд More … и Less … В режиме развернутого ответа пользователь получает информацию о представлении запрашиваемого числа в системах счисления с основаниями от 2 до 16. Кроме этого, можно получить представление числа 11,(3) в типах данных при двоичном кодировании не только с двойной, но и с одинарной и с четверной точностью рис. 7.2. При этом можно выбрать порядок нумерации байт от старшего к младшему (big-endian).
Пример 5. Запрос для целого числа вида
1100111_2
приводит к дополнительной информации о представлении числа 103 в типах данных, предназначенных для хранения целых чисел, например
unsigned 8-bit integer: 67 unsigned 16-bit integer: 0067 …
Кодирование текста
Рассмотрим примеры запросов о кодах символов к системе Wolfram|Alpha.
Пример 6. Найти последовательность десятичных кодов символов в таблице Unicode по заданной строке можно с помощью запроса вида
to character code "Science"
Результат выглядит следующим образом:
{83, 99, 105, 101, 110, 99, 101}.Если же использовать текст на русском языке, то результат может быть неправильным. Например, для запроса
to character code "Привет"
результат имеет вид:
{1055, 112, 1080, 1074, 1077, 1090}.Система Wolfram|Alpha не различает русскую букву "р" и латинскую букву "p", так как они имеют одинаковое написание, поэтому для слова "Привет" вместо кода буквы русского алфавита приведен код буквы латинского алфавита.
Пример 7. В качестве ответов на запросы character code 65 - 126 и character code 1040 - 1103 система Wolfram|Alpha возвращает фрагменты таблицы Unicode для десятичных кодов символов, принадлежащих указанным диапазонам. В данном случае они содержат символы латиницы
и кириллицы , соответственно.



