Структуры данных и алгоритмы

Рассматриваются основные структуры данных, которые описываются в виде алгебраических моделей типов данных. В таких моделях данные представляются как множества элементов, а операции над ними - как функции или отношения на множествах.

Структуры данных представляются в виде термов. Такое представление используется не только в алгебраическом моделировании типов данных, но и в декларативных языках программирования - логических и функциональных. Основные операции над структурами данных моделируются с помощью функций в облаке Wolfram (Wolfram Cloud).

Рассматривается понятие алгоритма. Приводятся примеры реализации алгоритмов с помощью правил преобразований в облаке Wolfram.

Для программирования используется язык Wolfram (Wolfram Language), известный по его использованию в системе компьютерной математики Wolfram Mathematica. Язык Wolfram является мультипарадигменным языком программирования, основанным на знаниях. Облако Wolfram обладает блокнотным интерфейсом и имеет доступ к встроенным алгоритмам и знаниям.

Основные структуры данных

Основными структурами данных являются линейные, иерархические и табличные. Структуры данных различаются методом адресации данных.

В линейных структурах доступ к данному осуществляется по индексу. Основными примерами линейных структур являются список, стек, очередь, дек, одномерный массив. Отличаются они операциями, которые можно производить над ними.

Иерархические структуры хранят частично упорядоченные данные. Примером является файловая структура - иерархическая структура хранения файлов на диске в специальных областях памяти, называемых каталогами или папками. Основным примером иерархической структуры является дерево.

В табличных структурах данных доступ к элементу осуществляется по двум индексам - номеру строки и номеру столбца. Примерами табличных структур являются двумерные массивы, таблицы в базах данных, матрицы и т. д.

Рассмотрим основные линейные, иерархические и двумерные структуры данных, а также примеры их моделирования - представления с помощью термов и определения основных операций над ними с помощью правил преобразования (переписывания термов).

Понятие терма определяется индуктивно. Терм - это переменная, константа или выражение вида 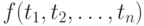, где f - функциональный символ арности n, а - термы.

В качестве среды для моделирования используется облако Wolfram. Оно предоставляет широкие возможности, но в данной главе используется только для определения функций с помощью правил вида lhs := rhs, где при вычислениях левая часть заменяется правой.

Определение термов и функций в языке Wolfram

Откроем новый файл в облаке Wolfram и переименуем его. Имя файла следует ввести в поле, обозначенное (unnamed). Система предложит присвоить файлу расширение nb. После написания имени следует нажать на символ галочки 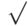, расположенный справа от поля ввода. Все файлы, включая безымянные, сохраняются в облаке.

Файл в облаке Wolfram состоит из набора ячеек. При введении кода автоматически создаются ячейки ввода, которым присваивается номер. Для того чтобы вычислить выражение, следует поместить курсор в ячейку, в котором оно находится, и использовать сочетание клавиш Shift+Enter. После этого создается ячейка вывода, в которую помещается результат. Например, введем выражение 2+2, затем нажмем Shift+Enter, в результате будем иметь:

In[1]:= 2+2 (  Shift+Enter  )
 Out[1]= 4

Между знаками ( и ) помещаются комментарии.

Имена встроенных функций пишутся с прописной (большой) буквы, поэтому для имен собственных функций ниже будут использоваться строчные (маленькие) буквы. Аргументы функции заключаются в квадратные скобки. Фигурные скобки используются для списков, а круглые - для группировки членов выражения.

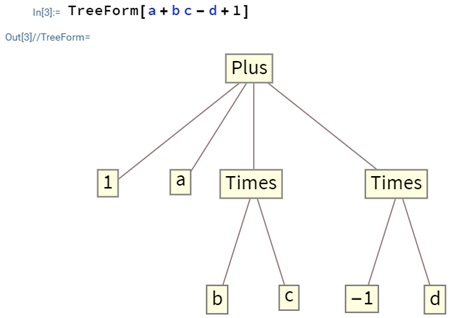
Любое выражение в языке Wolfram представляет собой терм - это переменная, константа или выражение вида f[expr1, expr2, …], где expr1, expr2, … - выражения. Символ f называется головой выражения. Представление выражения в виде терма возвращает функция FullForm:

 In[2]:=	FullForm[a+b c-d+1]
 Out[2]//FullForm= 	Plus[1, a, Times[b, c], Times[-1, d]]

Функция TreeForm представляет структуру выражения в виде дерева ( рис.6.1).

Рис. 6.1. Представление терма в виде дерева

Отметим, что вместо знака умножения можно использовать знак пробела: выражение 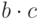соответствует b c (см. рисунок).

Если в одну ячейку введено несколько выражений, то после нажатия клавиш Shift+Enter, они будут вычислены последовательно. Для того чтобы значение выражения не выводилось, после выражения следует поставить знак точки с запятой (см. пример ниже).

Несколько запросов на вычисление могут быть объединены в список. Элементы списка заключаются в фигурные скобки и перечисляются через запятую. Результатом вычисления в этом случае является список с вычисленными элементами:

 In[4]:=	expr = cons[1, cons[2, cons[3, nil]]];
{FullForm[{1, 2, 3}], FullForm[expr]}
 Out[5]= 	{List[1, 2, 3], cons[1, cons[2, cons[3, nil]]]}

В языке Wolfram используется два вида присваиваний - абсолютное (=) и отсроченное (:=):

lhs = rhs и lhs := rhs

(lhs и rhs - сокр. от left hand side и right hand side). В первом случае объекту lhs присваивается вычисленное значение выражения rhs, а во втором - невычисленное. Как только в коде встретится объект lhs, в первом случае он заменится на ранее вычисленное значение выражения rhs, а во втором случае на только что вычисленное его значение.

Например, присвоим переменным u и v значение RandomInteger[10] с помощью различных видов присваиваний. Функция RandomInteger от аргумента R возвращает случайное число в пределах от 0 до R - 1 включительно. Последующее использование этих переменных приводит к результатам, показанным ниже:

 In[6]:=	u = RandomInteger[10];
v := RandomInteger[10]
{u, u, u, u, u}
{v, v, v, v, v}
 Out[8]= 	{1, 1, 1, 1, 1}
 Out[9]= 	{8, 3, 4, 1, 3}