Структуры данных и алгоритмы

Алгоритм преобразования дробной части числа из десятичного представления в p-ичное

Пусть [x] и {x} - целая и дробная части действительного числа x, соответственно. Обозначим через m число знаков после запятой представления дробной части числа в системе счисления с основанием p.

Псевдокод алгоритма перевода неотрицательного десятичного числа, меньшего единицы, в систему счисления с основанием p имеет вид:

n = 0,14, p = 2, m = 5, deque = []
цикл пока n > 0 и m > 0
n = n * p
	deque = addFront(deque, [n])
	n = {n}
	m = m - 1
конец цикла
печать deque

Определим функцию fracToP, которая возвращает первые m разрядов p-ичного представления неотрицательного числа n, меньшего единицы. Как и ранее, используем вспомогательную функцию:

Пример 4. Найдем первые 5 знаков после запятой двоичного представления числа 0,14 с помощью функции fracToP. Имеем:

На языке Wolfram код выглядит следующим образом:

 In[23]:= fracToP[n_, p_Integer?Positive, m_] := If[
0<=n<1 && m>=0 && p>1, g[n, p, m, nil], nil]
g[0, _, _, d_] := d
g[_, _, 0, d_] := d
g[n_, p_, m_, d_] := g[FractionalPart[n p], p, 
m - 1, addFront[d, IntegerPart[n p]]]
fracToP[0.14, 2, 5]
fracToP[0.7, 3, 6]
fracToP[0.238, 16, 5]
 Out[27]= cons[0, cons[0, cons[1, cons[0, cons[0, nil]]]]]
 Out[28]= cons[2, cons[0, cons[0, cons[2, cons[2, cons[0, nil]]]]]]
 Out[29]= cons[3, cons[12, cons[14, cons[13, cons[9, nil]]]]]

Встроенные функции IntegerPart и FractionalPart возвращают соответственно целую и дробную часть действительного числа.

Функцию decimalToP преобразования представления числа из десятичной системы счисления в систему счисления с основанием p можно определить следующим образом:

In[30]:= decimalToP[n_, p_, m_] := 
append[intToP[IntegerPart[n], p], 
cons[z, fracToP[FractionalPart[n], p, m]]]
append[nil, l_] := l
append[cons[h_, t_], l_] := cons[h, append[t, l]]
decimalToP[35.85, 2, 10]
 Out[33]=cons[1, cons[0, cons[0, cons[0, cons[1, cons[1, cons[z, 
cons[1, cons[1, cons[0, cons[1, cons[1, cons[0, 
cons[0, cons[1, cons[1, cons[0, nil]]]]]]]]]]]]]]]]]

Символ z в данном списке соответствует знаку запятой.

Алгоритм преобразования целой части числа из p-ичного представления в десятичное

Псевдокод алгоритма преобразования представления целого неотрицательного числа из p-ичной системы счисления в десятичную систему имеет вид:

deque = [1, 0, 1, 1, 0, 1, 1], p = 2, n = 0
цикл пока deque  []
n = n * p + rear(deque)
deque = removeRear(deque)
конец цикла 
печать n

Определение функции intToDec, которая по деку p-ичных цифр и основанию p системы счисления возвращает десятичное число, выглядит следующим образом:

Пример 5. Найдем десятичное число, двоичное представление которого равно с помощью функции intToDec. Имеем:

Определение функции intToDec на языке Wolfram имеет вид:

In[34]:= intToDec[d_, p_Integer?Positive] := h[d, p, 0]
h[nil, _, n_] := n
h[cons[a_, t_], p_, n_] := h[t, p, n p + a]
y = cons[1, cons[1, cons[0, nil]]];
intToDec[y, 2]
 Out[38]= 6

Алгоритм преобразования дробной части числа из p-ичного представления в десятичное

Псевдокод алгоритма преобразования представления дробной части рационального числа из системы счисления с основанием p в десятичное число выглядит следующим образом:

deque = [1, 0, 1, 1, 0, 1, 1], p = 2, n = 0
цикл пока deque  []
n = (n + front(deque)) / p
deque = removeFront(deque)
конец цикла 
печать n

Функция fracToDec преобразования дробной части числа из p-ичной в десятичную систему счисления определяется в виде:

Пример 6. Найдем десятичное число, двоичное представление которого равно 0,101 с помощью функции fracToDec. Имеем:

Определение функции fracToDec на языке Wolfram имеет вид:

In[39]:= fracToDec[d_, p_Integer?Positive] := r[d, p, 0]
r[nil, _, n_] := n
r[d_,p_,n_]:=r[removeFront[d],p,(n+front[d])/p]
fr = cons[1, cons[0, cons[1, nil]]];
fracToDec[fr, 2]
 Out[43]= 

Функцию toDecimal, которая преобразует p-ичное представление числа в десятичное, можно определить следующим образом:

In[44]:= toDecimal[d_, p_] := intToDec[getInt[d], p] +
fracToDec[getFract[d], p]
getInt[nil] := nil
getInt[cons[z, _]] := nil
getInt[cons[a_, t_]] := cons[a, getInt[t]]
getFract[nil] := nil
getFract[cons[z, t_]] := getInt[t]
getFract[cons[_, t_]] := getFract[t]
num = append[y, cons[z, fr]]
getInt[num]
getFract[num]
toDecimal[num, 2]
N[%]
 Out[51]= cons[1, cons[1, cons[0, cons[z, cons[1, cons[0, cons[1, nil]]]]]]]
 Out[52]= cons[1, cons[1, cons[0, nil]]]
 Out[53]= cons[1, cons[0, cons[1, nil]]]
 Out[54]=  
 Out[55]= 6.625

Функция N возвращает число в десятичном формате. Вместо знака % подставляется результат последнего вычисления.

Упражнения

1. Определите на языке Wolfram функцию вычисления наибольшего общего делителя двух целых чисел.

2. Определите на языке Wolfram для списков, представленных термами, операцию

   1. вычисления суммы элементов списка чисел;
   2. вычисления произведения элементов списка;
   3. вычисления среднего арифметического элементов списка чисел;
   4. вычисления числа вхождений заданного элемента в список;
   5. вычисления числа четных элементов в список;
   6. замены всех вхождений одного элемента на другой элемент;
   7. удаления первого вхождения заданного элемента в список;
   8. удаления всех вхождений заданного элемента в список;
   9. удаления элемента с заданным индексом;
   10. проверки принадлежности элемента списку;
   11. вычисления минимального элемента списка;
   12. вычисления максимального элемента списка;
   13. обращения списка ();
   14. возвращения списка элементов с четными индексами;
   15. вставки после каждого элемента его удвоенного значения;
   16. построения списка индексов всех вхождений элемента в список;
   17. построения списка случайных чисел, не превосходящих заданной величины, который состоит из заданного числа элементов;
   18. удаления дубликатов из списка ;
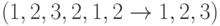   19. удаления подряд идущих дубликатов из списка .

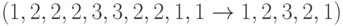3. Определите на языке Wolfram для бинарных деревьев, представленных термами, операцию

   1. вычисления суммы вершин дерева;
   2. вычисления числа вершин, равных заданному элементу;
   3. вычисления минимального элемента дерева;
   4. замены заданного элемента на другой элемент;
   5. удаления левого поддерева;
   6. удаления правого поддерева;
   7. построения списка листьев дерева;
   8. построения по списку дерева, в котором элементы левого поддерева каждой вершины меньше этой вершины, а элементы правого поддерева больше или равны ей.

4. Определите на языке Wolfram для произвольных деревьев, представленных термами, операцию

   1. вычисления суммы вершин дерева;
   2. вычисления числа вершин, равных заданному элементу;
   3. вычисления суммы четных вершин дерева;
   4. вычисления максимального элемента дерева;
   5. замены заданного элемента на другой элемент;
   6. построения списка листьев дерева.

5. Определите на языке Wolfram для матриц, представленных термами, операцию

   1. вычисления суммы элементов;
   2. вычисления минимального элемента матрицы;
   3. вычисления суммы элементов заданной строки;
   4. вычисления суммы элементов заданного столбца;
   5. сложения матриц;
   6. транспонирования матрицы;
   7. умножения матриц.
6. Реализуйте на языке Wolfram алгоритм пузырьковой сортировки для списков, представленных термами.
7. Реализуйте на языке Wolfram для списков, представленных термами, алгоритм перемешивания элементов списка случайным образом.
8. Реализуйте на языке Wolfram алгоритм построения треугольника Паскаля, используя списки, представленные термами.
9. Реализуйте на языке Wolfram алгоритм решения квадратного уравнения, который по списку коэффициентов уравнения возвращает список корней уравнения.

10. Реализуйте на языке Wolfram для многочленов, представленных списками коэффициентов по возрастанию степеней (списки представляются в виде термов), операцию

    1. сложения многочленов;
    2. умножения многочлена на число;
    3. произведения многочленов;
    4. дифференцирования многочлена;
    5. вычисления первообразной многочлена.