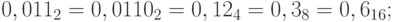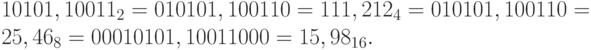Представление чисел в системах счисления
Пусть теперь в системе счисления с основанием p для целого неотрицательного числа x выполняется разложение
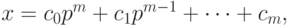
где m = k(n + 1) - 1, 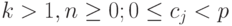 , для j = 0, 1, ..., m. Число слагаемых в правой части равенства кратно k. Разобьем их последовательно на группы, содержащие по k элементов (очевидно, что таких групп будет n + 1), в результате будем иметь:
, для j = 0, 1, ..., m. Число слагаемых в правой части равенства кратно k. Разобьем их последовательно на группы, содержащие по k элементов (очевидно, что таких групп будет n + 1), в результате будем иметь:
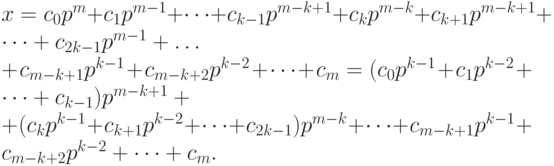
Положим
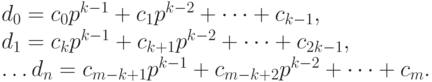
Ясно, что 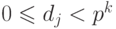 , для j = 0, 1, ..., n. Кроме того, m = kn + k - 1. Поэтому представление числа x в системе счисления с основанием
, для j = 0, 1, ..., n. Кроме того, m = kn + k - 1. Поэтому представление числа x в системе счисления с основанием 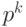 имеет вид:
имеет вид: 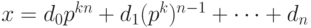
Таким образом, при преобразовании представления числа из системы счисления с основанием p в систему счисления с основанием 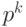 , достаточно сгруппировать буквы исходного слова в слова длины k, при необходимости добавив нули в начале слова, а затем заменить эти слова
, достаточно сгруппировать буквы исходного слова в слова длины k, при необходимости добавив нули в начале слова, а затем заменить эти слова
Пример 18. Для числа 73 по таблицам имеем:
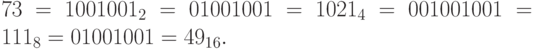
Преобразование дробной части числа, если она имеет конечное число знаков после запятой, выполняется аналогичным образом, так как
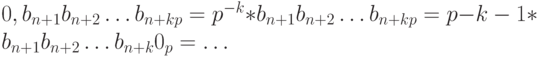
Очевидно, что для дробной части при преобразовании представления числа из системы счисления с основанием p в систему счисления с основанием 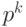 необходимое число нулей добавляется справа.
необходимое число нулей добавляется справа.
Пример 19. С помощью таблиц найдем двоичное представление чисел  ,
,  и
и  . Имеем:
. Имеем:
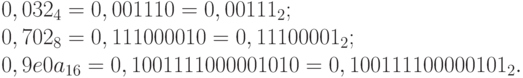
Пример 20. Найдем представление чисел 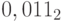 и
и 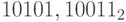 в системах счисления с основаниями 4, 8 и 16 с помощью таблиц:
в системах счисления с основаниями 4, 8 и 16 с помощью таблиц:
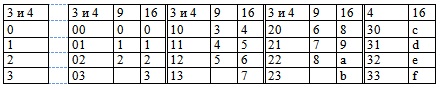
Ниже приведена общая таблица для преобразования чисел между системами счисления с основаниями 3 и 9, а также 4 и 16 ( Таблица ).
Пример 21. 1) Найдем для чисел  и
и 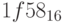 их троичное и четверичное представления, соответственно. По таблице h имеем:
их троичное и четверичное представления, соответственно. По таблице h имеем:

2) Представление чисел 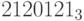 и
и  в системах счисления с основаниями 9 и 16, соответственно, по рис 1.2 находится следующим образом:
в системах счисления с основаниями 9 и 16, соответственно, по рис 1.2 находится следующим образом:
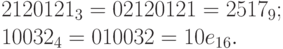
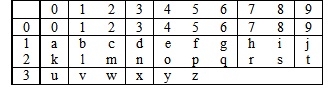
В системах счисления с основаниями от 11 до 36 включительно цифрами являются десятичные цифры и буквы латинского алфавита. Эти цифры приведены в табл.. Ячейка с индексами i и j содержит цифру, значение которой в десятичной системе равно 10i + j.
Пример 22. 1) Найдем шестеричное представление числа 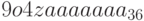 . Имеем:
. Имеем:  . Поэтому
. Поэтому
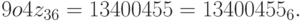
2) Найдем представление числа  в системе счисления с основанием 25. Имеем:
в системе счисления с основанием 25. Имеем: 
Следовательно,

В системах счисления с основанием 37 и более в качестве цифр часто используются десятичные числа. В этом случае цифры состоят из нескольких знаков. Мы в записи чисел будем просто разделять такие цифры пробелами (как в системе Wolfram|Alpha - см. гл. 7).
Пример 23. Вычислим 60-ричное представление числа 43000. Имеем:
43000 = 716 * 60 + 40; 716 = 11 * 60 + 56.
Таким образом, 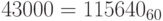 . Отсюда, в частности, следует, что 43000 секунд составляет 11 часов, 56 минут и 40 секунд.
. Отсюда, в частности, следует, что 43000 секунд составляет 11 часов, 56 минут и 40 секунд.
В вавилонской системе счисления c основанием 60 для записи цифр, от 1 до 59, использовались два знака: стоячий клин для обозначения 1 и лежачий для обозначения 10 ( рис. 1.1 (a)). Разряды отделялись пробелами, иногда для разделения цифр использовались специальные символы, по причине отсутствия нуля. В ней число 43000 могло быть записано так, как показано на рис. 1.4 (b).
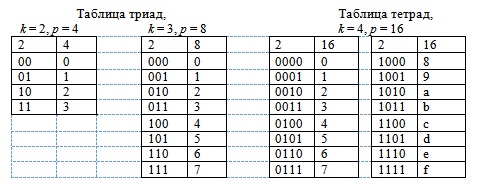
Рис. 1.4. Рис. 1.4. (a) Клинописное обозначение чисел 1 (слева) и 10 (справа); (b) представление числа 43000
Пример 24. Найдем семеричное представление числа  . Имеем:
. Имеем:  . Поэтому
. Поэтому
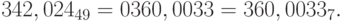
Пример 25. Найдем представление числа 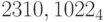 в системе счисления с основанием 64:
в системе счисления с основанием 64:
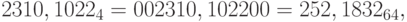
так как 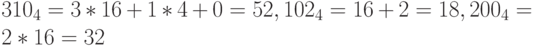 .
.
Упражнения
-
Запишите число 100 в системе счисления с основанием
a) 2;
b) 3;
c) 12;
d) 20;
e) 60.
-
Найдите двоичное представление числа
a) 1,1;
b) 7,7;
c) 14,14;
d) 33,3.
-
Представьте число 22,2 в системе счисления с основанием
a) 4;
b) 8;
c) 12;
d) 16.
- Найдите двоичное представление числа
 , ограничившись в его двоичном виде тремя знаками после запятой.
, ограничившись в его двоичном виде тремя знаками после запятой. - Определите, в какой системе счисления верно равенство
 .
. - Покажите, что в системе счисления с основанием p, где
 , число
, число  является кубом числа
является кубом числа  .
. -
Найдите десятичное представление числа
a)
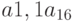 ;
;b)
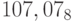 ;
;c)
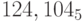 ;
;d)
 .
. -
Не используя (4), представьте в виде рациональной дроби число
a) 0,22(321);
b)

- Покажите, что если
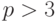 , то
, то  .
. -
Представьте в виде рациональной дроби число
a) 0,(023);
b) 0,0(7);
c)
 ;
;d)
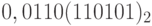 .
. - Определите число, предшествующее числу
 .
. - Найдите число, следующее за числом
 .
. -
Постройте 1) таблицу сложения; 2) таблицу умножения в системе счисления с основанием
a) 2;
b) 3;
c) 4;
d) 8;
e) 16.
-
Выполните операции сложения, вычитания, умножения и деления в системе счисления с основанием p для чисел
a)
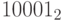 и
и  , p = 2;
, p = 2;b)
 и
и  , p = 16.
, p = 16. -
Выполните действия в троичной системе счисления:
a)
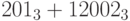 ;
;b)
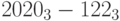 ;
;c)
 ;
;d)
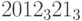 .
. -
Выполните действия в системе счисления с указанным основанием:
a)
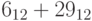 ;
;b)
 ;
;c)
 ;
;d)
 .
. -
Найдите представление числа x в системе счисления с основанием p, если
a)
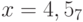 , p = 3;
, p = 3;b)
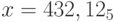 , p = 7.
, p = 7. - Используя таблицу тетрад, постройте таблицу для преобразования чисел между системами счисления 2 и 32.
-
Найдите представление числа
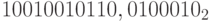 в системе счисления с основанием
в системе счисления с основаниемa) 4;
b) 8;
c) 16;
d) 32.
-
Найдите представление в двоичной системе счисления числа
a)
 ;
;b)
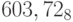 ;
;c)
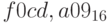 .
. -
Найдите представление в двоичной системе счисления числа
a)
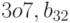 ;
;b)
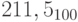 .
. -
Постройте общую таблицу
a) для преобразования чисел между системами счисления с основаниями 5 и 25, а также 6 и 36;
a) для преобразования чисел между системами счисления с основаниями от 2 до 6 включительно и системами счисления с основаниями, равными квадратам этих чисел, т. е. с основаниями 4, 9, 16, 25 и 36, соответственно;
-
Найдите представление числа x в системе счисления с основанием p, если
a)
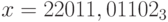 , p = 9;
, p = 9;b)
 , p = 3;
, p = 3;c)
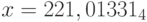 , p = 16;
, p = 16; d)
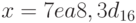 , p = 4;
, p = 4;e)
 , p = 25;
, p = 25;f)
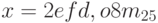 , p = 5;
, p = 5;g)
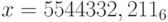 , p = 36;
, p = 36;h)
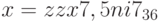 , p = 6.
, p = 6. -
Постройте таблицу для преобразования чисел между системами счисления
a) 4 и 64;
b) 8 и 64;
c) 7 и 49.
-
Найдите представление числа x в системе счисления с основанием p, если
a)
 , p = 100;
, p = 100;b)
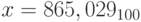 , p = 10;
, p = 10;c)
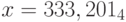 , p = 64;
, p = 64;d)
 , p = 4;
, p = 4;e)
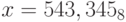 , p = 64;
, p = 64;f)
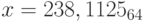 , p = 8;
, p = 8;g)
 , p = 49;
, p = 49;h)
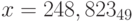 , p = 7;
, p = 7;i)
 , p = 64;
, p = 64;j)
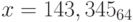 , p = 2;
, p = 2;k)
 , p = 60;
, p = 60;l)
 , p = 10.
, p = 10.