Представление чисел в системах счисления
Имеем: 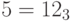 . В троичной системе счисления
. В троичной системе счисления
Таким образом,  . Но
. Но 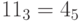 , а
, а 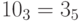 . Поэтому
. Поэтому 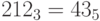 .
.
Для дробной части числа в троичной системе счисления имеем:
Таким образом,  , и т. д. Следовательно,
, и т. д. Следовательно, 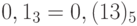 , так как
, так как 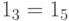 , а
, а 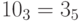 . В результате получается, что
. В результате получается, что 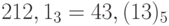 .
.
Выполним обратное преобразование: найдем троичное представление числа 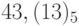 . В пятеричной системе счисления
. В пятеричной системе счисления
Таким образом, 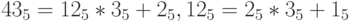 .
.
Поэтому 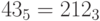 .
.
Далее, 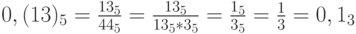 .
.
Следовательно, 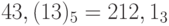 .
.
Таблицы и преобразование чисел
Рассмотрим методы преобразования представления числа между системами счисления с основаниями p и 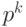 с помощью таблиц. Таблица содержит упорядоченный набор слов длины
с помощью таблиц. Таблица содержит упорядоченный набор слов длины  в алфавите из p букв. Эти буквы соответствуют цифрам в системе счисления с основанием p, а слова - цифрам в системе счисления с основанием
в алфавите из p букв. Эти буквы соответствуют цифрам в системе счисления с основанием p, а слова - цифрам в системе счисления с основанием 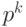 .
.
Понятие алфавита, слова и языка
Алфавит - конечное множество, элементы которого называются буквами. Конечная последовательность букв называется словом. Множество всех слов над алфавитом A обозначается A*. Язык - это подмножество множества слов. Число букв в слове называется длиной слова. Пустое слово обозначается  , длина пустого слова равна 0.
, длина пустого слова равна 0.
Рассмотрим алфавит, состоящий из двоичных цифр: A = {0, 1}. Один двоичный разряд представляет один бит. Если разрядов k, то с их помощью можно записать 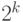 различных последовательностей 0 и 1 - слов над алфавитом A. Слова над алфавитом /{0, 1/} называются двоичными словами.
различных последовательностей 0 и 1 - слов над алфавитом A. Слова над алфавитом /{0, 1/} называются двоичными словами.
Порядок следования слов в словаре называется лексикографическим. Например, в таком порядке в словаре размещаются слова а, абажур, абак, аббат, аббатство, аббревиатура, аберрация, абзац.
Лексикографический порядок определяется следующим образом. Пустое слово меньше непустого. Если первая буква первого слова меньше первой буквы второго слова, то первое слово располагается раньше второго. Если первые буквы слов совпадают, то сравнение производится по вторым буквам, и т. д. Например, в алфавите /{0, 1/} буква 0 меньше, чем буква 1, поэтому слова, начинающиеся на 0, в словаре двоичных слов должны располагаться раньше, чем слова, которые начинаются на 1.
В общем случае, пусть p - целое число, такое что p > 1, и алфавит A содержит p букв со значениями от 0 до p - 1:
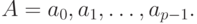
Будем считать, что 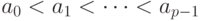 . Всего над алфавитом A существует
. Всего над алфавитом A существует 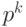 слов длины k, так как на каждой из k позиций в слове может стоять любая из p букв. Поэтому набор этих слов соответствует цифрам в системе счисления с основанием
слов длины k, так как на каждой из k позиций в слове может стоять любая из p букв. Поэтому набор этих слов соответствует цифрам в системе счисления с основанием 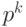 .
.
Замечание. Пусть 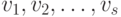 , где
, где  , - упорядоченное множество слов длины n над алфавитом A. Тогда упорядоченное множество слов длины n + 1 имеет вид:
, - упорядоченное множество слов длины n над алфавитом A. Тогда упорядоченное множество слов длины n + 1 имеет вид:
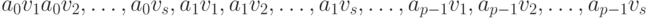
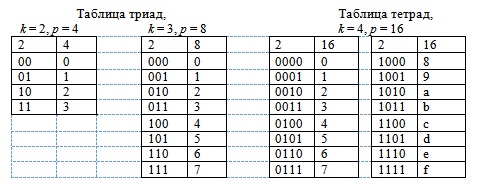
Таблицы триад и тетрад
Пусть p = 2 и A = /{0, 1/}. Имеем:
- упорядоченный набор слов длины 0;
0, 1 - упорядоченный набор слов длины 1;
00, 01, 10, 11 - упорядоченный набор слов длины 2, и т. д.
Слова длины 3 и 4 называют триадами и тетрадами, соответственно.
Ниже приведены таблицы двоичных слов длины k, для k = 2, 3 и 4 ( рис. 1.1), и соответствующих им цифр в системе счисления с основанием 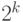 , которые представляют эти слова. В заголовке каждого столбца указывается основание системы счисления, которой принадлежат слова, содержащиеся в столбце.
, которые представляют эти слова. В заголовке каждого столбца указывается основание системы счисления, которой принадлежат слова, содержащиеся в столбце.
Таблицы используются для быстрого преобразования представления числа между двоичной системой счисления и системами счисления с основаниями 4, 8 и 16.
Системы счисления с основаниями p и степенями p
Рассмотрим представление чисел в системах счисления с основаниями p и 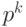 , для k > 1.
, для k > 1.
Положим 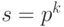 . Для целого неотрицательного числа x имеем:
. Для целого неотрицательного числа x имеем:
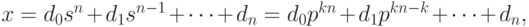
где 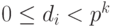 , для i = 0, 1, ..., n. Но
, для i = 0, 1, ..., n. Но 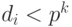 , поэтому в системе счисления с основанием p для цифр
, поэтому в системе счисления с основанием p для цифр 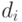 выполняются следующие разложения:
выполняются следующие разложения:
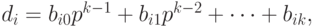
где 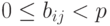 , для j = 0, 1, ..., k, i = 0, 1, ..., n. Соответственно, в системе счисления с основанием p число
, для j = 0, 1, ..., k, i = 0, 1, ..., n. Соответственно, в системе счисления с основанием p число 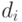 имеет представление
имеет представление 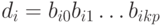 .
.
Подставим указанные выше разложения для чисел 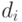 в разложение для числа x, в результате будем иметь:
в разложение для числа x, в результате будем иметь:
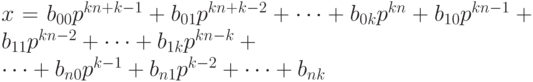
Поэтому число x в системе счисления с основанием p имеет следующее представление:
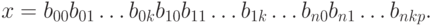
Таким образом, если число в системе счисления с основанием 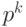 имеет представление
имеет представление  , то для того, чтобы найти его представление в системе счисления с основанием p, достаточно каждую из цифр
, то для того, чтобы найти его представление в системе счисления с основанием p, достаточно каждую из цифр 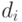 , для i = 0, 1, ..., n, заменить ее представлением в системе счисления с основанием p с помощью слова длины k.
, для i = 0, 1, ..., n, заменить ее представлением в системе счисления с основанием p с помощью слова длины k.
Пример 16. С помощью таблиц найдем представление чисел  ,
,  и
и  в двоичной системе счисления. Имеем:
в двоичной системе счисления. Имеем:
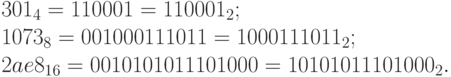
Пример 17. Представление чисел 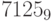 и
и  в троичной системе счисления можно найти следующим образом:
в троичной системе счисления можно найти следующим образом:
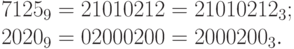
Проведенные выше преобразования с помощью знака суммирования  можно записать в виде:
можно записать в виде:
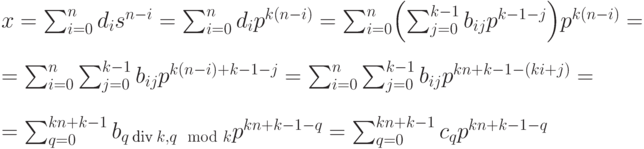
В предпоследнем равенстве выполнен переход от двойного суммирования к суммированию по одному индексу с помощью замены q = ki + j. Индексы i и j меняются от 0 до n и от 0 до k - 1, соответственно, поэтому индекс q последовательно принимает все значения от 0 до kn + k - 1. Далее, учитывая, что  , получим: i = q div k, j = q mod k. В последнем равенстве приведенного выше выражения выполнен переход от двойных индексов к одинарным:
, получим: i = q div k, j = q mod k. В последнем равенстве приведенного выше выражения выполнен переход от двойных индексов к одинарным:  . Итак, имеем:
. Итак, имеем: