Представление чисел в системах счисления
В конструкции вычислительных устройств ключевую роль играют системы счисления. Первые механические счетные машины были разработаны на основе десятичной системы счисления. Применение вместо нее двоичной системы позволило существенно уменьшить размеры механических счетных устройств. В истории известны случаи использования для вычислений различных систем счисления, например, шестидесятеричной древневавилонской, смешанной римской, непозиционной десятичной древнеегипетской и др.
В современных компьютерах для представления данных и вычислений используется двоичная система счисления. Тем не менее, актуальным является изучение способов применения и других систем счисления.
В настоящей главе рассматриваются традиционные позиционные системы счисления с целым положительным основанием, методы преобразования представления действительного числа между десятичной и другими системами счисления, а также между системой счисления с основанием p и системой счисления с основанием, являющимся степенью p. Обсуждаются арифметические операции в системах счисления.
Позиционные системы счисления
Система счисления - символический метод представления чисел с помощью письменных знаков. Эти знаки, или группы знаков, называются цифрами. Если число представляется в виде последовательности цифр, и значение цифры зависит от ее позиции, или разряда в этой последовательности, то система счисления называется позиционной. Позиционная система счисления называется p-ичной, если для представления чисел в ней используется p цифр со значениями от 0 до p - 1 включительно, а значения разрядов определяются степенями числа p. Число p называется основанием системы счисления.
Пусть p - целое число, p> 1. Неотрицательное действительное число x может быть разложено по степеням числа p следующим образом:
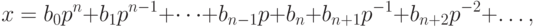 |
( 1) |
где 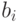 - целые числа,
- целые числа, 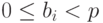 , для i = 0, 1, 2, ...; числа
, для i = 0, 1, 2, ...; числа 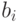 называются коэффициентами при степенях числа p. Запись числа x в виде
называются коэффициентами при степенях числа p. Запись числа x в виде
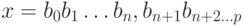
где вместо чисел 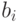 могут использоваться заменяющие их знаки, называется представлением числа x в p-ичной системе счисления, или p-ичным представлением, а также p-ичным числом или представлением в p-ичном виде. Если p = 10, то символ p обычно опускается. Знаки, которые используются для обозначения чисел
могут использоваться заменяющие их знаки, называется представлением числа x в p-ичной системе счисления, или p-ичным представлением, а также p-ичным числом или представлением в p-ичном виде. Если p = 10, то символ p обычно опускается. Знаки, которые используются для обозначения чисел 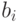 , называются цифрами.
, называются цифрами.
В дальнейшем в p-ичном представлении числа, приведенном выше, будут использоваться как сами числа 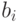 , так и обозначающие их цифры. Различие обозначений будет ясно из контекста.
, так и обозначающие их цифры. Различие обозначений будет ясно из контекста.
Пример 1. В двоичной системе счисления для представления чисел используются цифры 0 и 1, в троичной - 0, 1 и 2, в шестнадцатеричной - цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e и f. Значения последних шести цифр соответственно равны 10, 11, 12, 13, 14 и 15.
Если дробная часть числа имеет период, то его заключают в круглые скобки, в виде

Пример 2. Число 7,8 можно представить следующим образом:
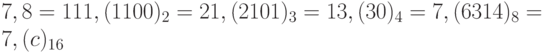
Пример 3. Найдем представление числа 9,625 в двоичной системе счисления. Имеем: 9,625 = 9 + 0,625 = 8 + 1 + 0,5 + 0,125. Поэтому разложение этого числа по степеням 2 имеет вид:
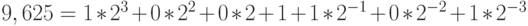
Следовательно, 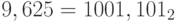 .
.
Пример 4. Найдем десятичное представление числа 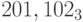 :
:
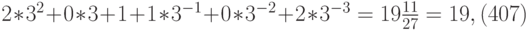
Преобразование десятичных чисел в p-ичные
Пусть действительное число x имеет разложение (1). Обозначим через xint - целую часть числа x, а через xfract - дробную:
xint = [x], xfract = {x}
так что x = xint + xfract. Тогда в системе счисления с основанием p представление целой и дробной части числа x соответственно имеет вид:
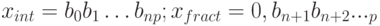
Пусть a и b - целые числа и b не равно 0. Обозначим через a div b - целую часть частного, а через a mod b - остаток от деления a на b.
1. Преобразование целой части числа. Из разложения (1) следует, что целая часть числа x выглядит следующим образом:
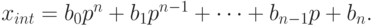
Поэтому 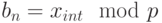 . Далее,
. Далее,  , так что аналогичным образом можно найти коэффициент
, так что аналогичным образом можно найти коэффициент 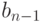 , и т. д.
, и т. д.
Положим 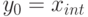 . Имеем:
. Имеем:
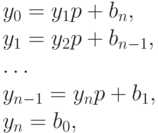 |
( 2) |
где 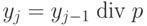 , для
, для 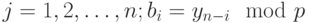 , для
, для 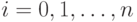 . Данный способ вычисления коэффициентов
. Данный способ вычисления коэффициентов 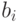 соответствует методу деления "уголком":
соответствует методу деления "уголком":
Пример 5. Представление числа 73 в троичной системе счисления можно найти следующим образом (ср. с делением "уголком"):
73 = 24 * 3 + 1; 24 = 8 * 3 + 0; 8 = 2 * 3 + 2.
Поэтому 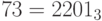 .
.
Другим способом вычисления представления целого числа 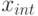 в системе счисления с основанием p является метод выделения полных степеней, в котором операции целочисленного деления применяются к максимальной степени числа p, не превосходящей
в системе счисления с основанием p является метод выделения полных степеней, в котором операции целочисленного деления применяются к максимальной степени числа p, не превосходящей 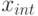 , коэффициент разложения находится как частное от деления, затем вычисления продолжаются для остатка от деления. Положим
, коэффициент разложения находится как частное от деления, затем вычисления продолжаются для остатка от деления. Положим 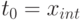 . Имеем:
. Имеем:
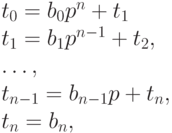
где 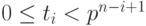 , для
, для 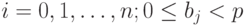 , для
, для  .
.
В этом методе удобно использовать таблицы степеней.
Пример 6. Найдем троичное и двоичное представления числа 173.
- Заметим, что 81 < 173 < 243. Имеем: 173 = 2 * 81 + 11; 11 = 9 + 2. Поэтому
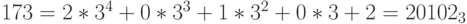 ;
; -
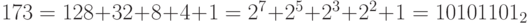 .
.
2. Преобразование дробной части числа. Дробная часть числа x, в соответствие с разложением (1), выглядит следующим образом:
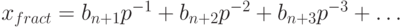
Заметим, что если умножить 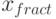 на p, то целая часть результата будет равна
на p, то целая часть результата будет равна 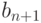 , а дробная часть будет иметь вид
, а дробная часть будет иметь вид 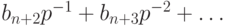 Коэффициент
Коэффициент  из разложения дробной части можно найти аналогичным образом, и т. д.
из разложения дробной части можно найти аналогичным образом, и т. д.
Положим 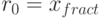 . Для первых m знаков после запятой имеем:
. Для первых m знаков после запятой имеем:
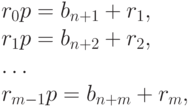
где ![b_{n + i} = [r_{i - 1}p], r_i = {r_{i - 1}p}](/sites/default/files/tex_cache/24a6337a9d9839ccd2f3fdfa1a83117d.png) , для i = 1, 2, ..., m. Очевидно, что
, для i = 1, 2, ..., m. Очевидно, что  , для j = 0, 1, ..., m.
, для j = 0, 1, ..., m.
Пример 7. Найдем троичное представление числа 0,7. Имеем:
0,7 * 3 = 2 + 0,1; 0,1 * 3 = 0 + 0,3; 0,3 * 3 = 0 + 0,9; 0,9 * 3 = 2 + 0,7; 0,7 * 3 = 2 + 0,1, и т. д.
Следовательно,  .
.
Для вычислений удобно использовать таблицы. В табл. 1.1 приведены вспомогательные вычисления для преобразования трех чисел: 0,7 - в троичную систему счисления, - в восьмеричную и 0,9 - в двоичную. Каждому числу соответствует столбец таблицы, серым цветом в каждом столбце выделен период.
- в восьмеричную и 0,9 - в двоичную. Каждому числу соответствует столбец таблицы, серым цветом в каждом столбце выделен период.
| p=3 | p=8 | p=2 |
|---|---|---|
| 0,7 |  |
0,9 |
| 2,1 | 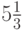 |
1,8 |
| 0,3 | 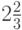 |
1,6 |
| 0,9 | 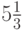 |
1,2 |
| 2,7 | 0,4 | |
| 2,1 | 0,8 | |
| 1,6 |
Таким образом,  ,
, 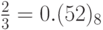 ;
; 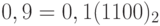 .
.