Вероятностные и компактные генетические алгоритмы
8.1. Вероятностные генетические алгоритмы
Рассмотрим представление популяции вектором вероятностей на следующем примере для трех различных популяций состоящих из четырех хромосом дан ниже:
Здесь популяция, состоящая из двоичных хромосом, представляется вектором 
, каждый элемент которого устанавливает относительную частоту появления гена "1" на соответствующей позиции.
Впервые такое представление было введено в [1] (Equilibrium Genetic Algorithm) и взято за основу в последующих работах [2,3,4,5,6]. В [1] на этой основе проведены теоретические исследования вопросов сходимости ГА и показано, что для ряда классических задач вероятностный ГА дает результаты, не уступающие стандартному ГА с однородным кроссинговером и стратегией элитизма при отборе родителей.
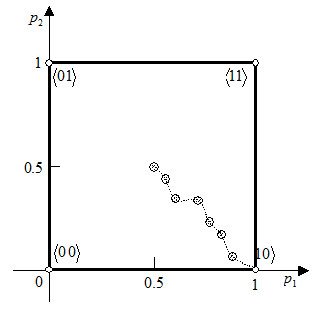
В этом случае эволюция популяции соответствует траектории в гиперкубе пространства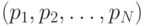 
. Траектория начинается в середине единичного гиперкуба (
для всех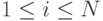 
) и заканчивается в одной из его вершин, которая соответствует найденному решению (двоичному коду), как это показано на рис.8.1.
В классическом ГА популяция представляется множеством двоичных векторов и изменяется путем применения операторов репродукции, кроссинговера и мутации. "Вероятностный" ГА работает не с исходной популяцией (множеством двоичных векторов), а непосредственно с ее вероятностным представлением – вектором вероятностей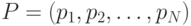 
. В этом случае [1] генетические операторы выполняются следующим образом.
Репродукция. В соответствии с текущим распределением вероятностей генерируется некоторое (относительно небольшое) множество двоичных векторов – особей. Для каждой из построенных особей вычисляется значение фитнесс-функции. Затем вектор вероятностей сдвигается в сторону особи 
(вершины гиперкуба), имеющей лучшее значение фитнесс-функции: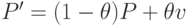 
. Здесь 
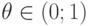– фиксированное вещественное число. Если несколько особей имеют наилучшее значение, то случайным образом выбирается одна из них.
Мутация. Каждая координата вектора корректируется случайным образом с вероятностью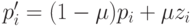 
, где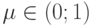 
– вещественный параметр, а 
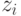принимает значения и с равной вероятностью. Таким образом, 
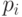сдвигается на небольшое расстояние в направлении или в соответствии со случайным значением 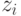. В [1] показано, что оператор кроссинговера в этом случае не является необходимым.
Очевидно, что из построенного вектора вероятностей легко получить двоичный вектор, представляющий решение задачи. Если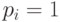 
(или близко к 1), то значение гена 
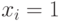, в противном случае 
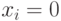. Эксперименты показали, что для некоторых задач этот подход дает результаты, сравнимые с классическим ГА при меньших затратах вычислительных ресурсов.